AND Probability Calculator

Head after head, that's the beginning of a lucky streak; but how do you define and calculate the probability of such events? Follow Omni in this tool dedicated to calculating the joint probability of two events.

What are you going to learn in this article?

• A short introduction to probability and a detailed explanation of what joint probability is. The conditions required and the formula we use when we learn how to find the probability of A and B, a generic pair of events.

• Examples and explanations of mathematical applications and real-world use of the joint probability formula. And much more!

To define the probability of multiple events, it's better to define what is probability first.

Probability is the likelihood of the outcome of a particular event. For example, the probability of getting a head in a coin toss is $P(\mathrm{head}) = 0.5$.

Where does this number come from? Super easy: toss the coin many, many times, and count the number of times you get a head, then divide this number by the number of launches. Say you throw it $100$ times: we got head $52$ times: $P(\mathrm{head}) = 0.52$. Try again! After another 100 flips you get $49$ heads: $P(\mathrm{head}) = 0.49$.

Increase the number of tosses (though it will take time!): in a million launches, we counted $499607$ heads. This is our $0.5$ probability.

When the number of outcomes is defined, we can also notice that the sum of the probabilities is $1$. $P=1$ is a particular probability: it represents an event we're sure will happen. The probability of obtaining either head or cross in a coin toss is $1$ since either one of the events will happen. Au contraire, $P=0$ represents an event that won't happen.

When considering multiple events, we can apply simple mathematical rules to calculate their joint probability, that is, the probability of both events to happen.

To calculate the joint probability of A and B, we need to impose an important condition: their independence. Two (or more) events are said to be independent if the outcome of each of them doesn't affect the others. For example:

• Throwing a die ten times represent ten separate, independent events; but

• Throwing ten dies at the same time in the same box represents events that influence each other: they are not independent.

The formula to calculate the joint probability of A and B (independent events) is:

We can also mark the joint probability with the notation $P(A,B)$. The symbol $\cap$ is the intersection.

The best way to understand the "and" probability formula is with sets, also known as Venn diagrams.

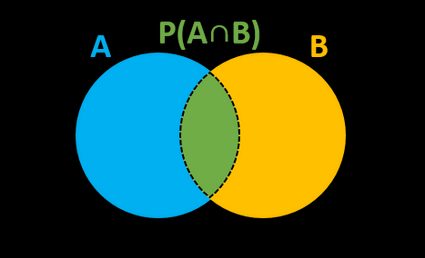
We are interested in the green area where the two sets intersect. That's where both events happen. Remember that Venn diagrams are purely a qualitative means to convey information but can't give you quantitative information about the values of the probabilities involved.

In case you have multiple events, you can calculate the joint probability by multiplying together the probability of every single event:

The formula for the probability of A and B is straightforward. It's time to see it in action.

Say you want to calculate the probability of obtaining two $6$'s from two die tosses. That would be luck, right?

First, define the probability to get a $6$ on the first die. Since there are six possible results, and we assume the die to not be tampered with, we say that:

To find the probability of two sixes, we just need to multiply the probability of getting six two times:

You can express this result in percentage:

To give you some context, you are more likely to get five times heads in a row while tossing a coin than two sixes in two rolls:

It may happen that your events are not independent. In that case, the outcome of one event would affect the outcome of the other. If you want to calculate the joint probability of such events, you can't directly multiply the probability of the individual events, but consider a quantity called conditional probability.

The conditional probability of A given B, written $P(A|B)$, is the probability of the outcome A for the first event in case the other event had outcome B. We use this quantity to find $P(A\cap B)$ in the formula:

As you can see, this is a modification of the original multiplication rule. You can also calculate the same quantity but considering a different "order" of the events:

The result is the same. How do you calculate the conditional probability? We're glad you asked: we have a tool for that purpose! Visit Omni's conditional probability calculator to learn everything about this useful quantity.

Probability and statistics are, we know, complex topics, often badly taught in school or directly overlooked. That's why Omni created a small suite of focused tools to help you with your problems and homework. Try our other probability calculators:

• The probability calculator; and
• The OR probability calculator.