Duckworth Lewis Calculator

This Duckworth Lewis calculator will help you decide which cricket team (but not a chirping cricket 😀) won the match, or you can use it to set a target for the second team if the game is interrupted by the rain.

This calculation is not as simple as you might think, as it's affected by human nature. We use an algorithm called the Duckworth-Lewis method to take into account how aggressively the teams will play, depending on the resources available to them. We will explain how the Duckworth-Lewis method works, based on when in play the interruption happens.

You'll find a full set of instructions and some examples of how the calculator works, so there's no need to be confused by the Duckworth-Lewis method anymore.

Both teams get 50 overs each in which to score as many runs as possible in regular one-day cricket while not losing more than ten wickets. Everything is OK as long as the sun continues to shine. But oh no! It's started to rain 🌧 The players come off the field, and the covers go on. Everyone waits until it stops raining and the ground is dry enough to play on again. But a couple of hours have gone by, and the sun is setting soon.

The organizers decide to cut the number of overs of the second innings to avoid playing in the dark. But how many runs does the chasing team now need to win the match? It's not their fault that the match was interrupted. 🤔

One way to solve the problem is to cut the run target in direct proportion to the number of overs available. So if Team 1 scores 200 runs from 50 overs and Team 2 is given 25 overs, merely using the run rate per over would say that they only need 101 runs to win.

The problem with this idea is that it doesn't take into account the reaction of the players. Knowing that they only have 25 overs, they will tend to play more aggressively than if they had the full 50 overs to score runs. Aggressive play is riskier – you might score more, but there is a greater chance of losing wickets. So the 101 run target will probably be too easy.

This is an excellent place to learn how the Duckworth Lewis method works. The Duckworth Lewis method attempts to calculate a statistically fair target, which has the same difficulty as the original target. It looks at the two resources available to both teams – overs and wickets. The Duckworth Lewis algorithm adjusts the run target in proportion to these resources.

You might have encountered the abbreviation DLS while looking for the Duckworth Lewis method. What is the DLS method? While commonly known as the Duckworth Lewis method, its official name since 2014 is the Duckworth-Lewis-Stern method (DLS), as this was when Frank Duckworth and Tony Lewis retired, and Professor Steven Stern took over to look after the algorithm.

Let's now look at how the Duckworth Lewis method is calculated in detail. At the start of the match, each team has 50 overs and 10 wickets. We say that both teams have 100 percent of the resources that they need to use to score as many runs as possible. A delay, early finish, or interruption will reduce a team's resources and mean they no longer have the same resources available.

To calculate a fair target for Team 2 to achieve, the Duckworth Lewis method uses the following equation:

Teams 2's par score = Team 1's score × (Team 2's resources / Teams 1's resources)

We round up this par score to the nearest integer to get the target Team 2 needs to win the match. For example, a rain delay means Team 2 only has 80% resources, while Team 1 played their innings without interruption (100% resources) and scored 231 runs. Putting these values into the equation above, we get:

Teams 2's par score = 231 × (80% / 100%) = 184.8

This means that Team 2 only needs 185 runs to win the match.

To find the total percentage of the resources each team has, given the number of overs available and wickets lost, we use a lookup table for the Standard Edition of the Duckworth Lewis method:

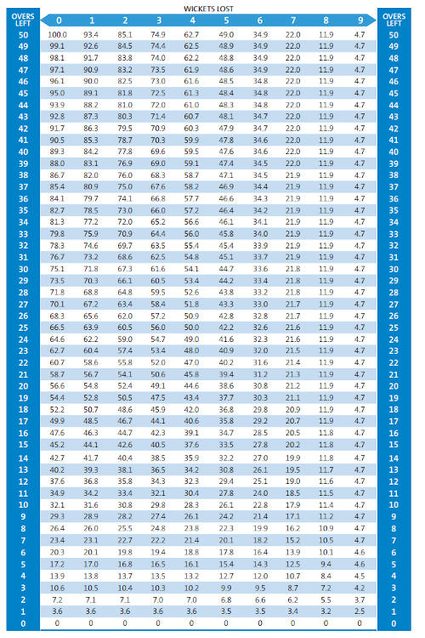
With DLS explained, you shouldn't struggle to set a fair target for the second team anymore. Remember, you can always use the Duckworth Lewis calculator to handle all the complicated computations.

Here are some common situations and how to calculate a team's resources using the above lookup table.

• There is a delay in a team's innings, and 50 overs have been reduced to 30. Of course, the team still has 10 wickets (0 wickets lost). From the table, we see that the corresponding value is 75.1% of resources left.

• There is an interruption to a team's innings, and they never resume play. Say this happens with 20 overs left, and they have lost 2 wickets (so there are 8 remain). Looking at the table, we get a figure of 52.4%, which is the amount of lost resources. So the amount of resources the team used is 100% - 52.4% = 47.6%.

• This time play is interrupted, but the team resumes their innings. Play stopped with 40 overs and 2 wickets lost (8 remaining). The game then resumes with 20 overs to play. Looking up 40 overs and 2 wickets lost, we see a figure of 77.8%. For 20 overs and 2 wickets lost, it is 52.4%. To find the resources used by the team, its 100% - 77.8% + 52.4% = 74.6%

If Team 2's resources are less than Team 1's, then we reduce the target for Team 2 using the equation:

Team 2's par score = S × (R2 / R1)

where:

• S – Number of runs Team 1 scored;
• R1 – Resources available to Team 1; and
• R2 – Resources available to Team 2.

If both teams' resources are the same, then no adjustment in the run target for Team 2 is required.

If Team 2 has more resources than Team 1, then we increase the run target using the following formula:

Team 2's par score = S + G50 × (R2 - R1)/100

where:

• G50 – Average score expected from the team batting first.

Given the extra resources, the formula asks what additional score could we expect? The value of G50 will depend on the level of competition. Our DLS calculator has a default of 245 runs, which applies to international and county cricket. Based on past results, you should update this value if you use it with your local village cricket team.

This calculator supports interruptions at the start, end, and middle of an innings. Let's go through some example situations and see how the Duckworth Lewis method is calculated to find an adjusted target for Team 2. If the match has already finished, you can enter the number of runs Team 2 scored and see if they won, lost, or drew the game, according to the DLS method.

Team 2's innings delayed

Rain, before play started, reduces the match to 30 overs each. Team 1 score 231 from their 30 overs. Due to a further delay, Team 2's innings is reduced to 28 overs. Here's how to use our calculator to find the target for Team 2:

1. Select Team 2's innings delayed from the "Interruption" option.
2. Enter 30 into Team 1's "Overs available".
3. Input 231 to tell the calculator how many runs Team 1 scored.
4. Enter 28 into Team 2's "Overs available" variable.
5. The calculator shows that Team 2 needs 221 runs to win, according to the DLS method.
6. If you enter the number of runs Team 2 actually achieved, the calculator tells you how much each team won the match by or if the match was a draw.

Let's see how you would calculate that result manually. Looking up 30 overs and 0 wickets left in the table, we get a resource value of 75.1%. For 28 overs and 0 wickets, it's 71.8%. Since Team 2's resources are less than Team 1's, we use the following equation:

Team 2's par score = S × (R2/R1) = 231 × (71.8/75.1) = 220.85

Rounding this up, we get a target to win for Team 2 of 221 runs.

Team 2's innings cut short

It's mid-afternoon, and it's just started to rain. Looking at the forecast, it's not going to stop anytime soon. It seems like that's the end of any play today. So who won? No worries - here comes the Duckworth Lewis algorithm to the rescue!

Team 1 scored 268 runs from 50 overs, while Team 2 got to 229 runs from 45 overs and lost 6 wickets. Using our Duckworth Lewis calculator, let's see if Team 2 won.

1. Select Team 2's innings cut short from the "Interruption" option.
2. Enter 50 overs and 268 runs for Team 1.
3. Enter 45 overs and 6 wickets lost for Team 2.
4. We get a target of 230 runs for Team 2 to win the match.
5. Entering Team 2's 229 runs, we see that the match is a draw, according to the Duckworth Lewis algorithm.

Calculating this result manually using the resources table, we first lookup the resources Team 2 couldn't use. They had 5 overs left after losing 6 wickets, corresponding to 14.3% of resources. Therefore, Team 2 used 100% - 14.3% = 85.7% during their innings. Calculating Team 2's par score:

Team 2's par score = S × (R2/R1) = 268 × (85.7/100) = 229.68

We round up to get the winning target of 230 runs and round down to get the draw score, which Team 2 scored on this occasion.

Team 2's innings interrupted

Team 1 scored 273 from their uninterrupted innings. Team 2 got to 70 runs from 19 overs and had lost 2 wickets when rain stopped play. When play resumed, Team 2's total overs were reduced to 36, so they had 17 overs available for the remainder of their innings. Here's how to use the Duckworth Lewis calculator to find Team 2's target.

1. Select Team 2's innings interrupted from the "Interruption" option.
2. Enter 50 overs and 273 runs for Team 1.
3. Enter 50 overs available for Team 2.
4. At the start of the interruption, 19 overs had been played, leaving 50 - 19 = 31 overs available.
5. Input with the number of wickets lost, 2.
6. Enter the number of overs remaining at the resumption of play, which is 36 - 19 = 17 overs.
7. Team 2 needs 214 runs to win. Enter the number of runs Team 2 actually got to see by how many runs they won or lost by (or if they drew).

To calculate manually, look up resource values for 31 and 17 overs left and 2 wickets off. Then compute the resources available to Team 2:

Resources available = 100% - Resources remaining at interruption + Resources remaining at restart

100% - 68.6% + 46.7% = 78.1%

We calculate Team 2's par score by doing:

Team 2's par score = S × (R2/R1) = 273 × (78.1/100) = 213.21

Round up to 214 to get the target for Team 2 to win the match.

Team 1's innings interrupted

This time Team 1's innings is interrupted by rain. The interruption happens after 34 overs, leaving 16 overs remaining, and Team 1 has lost 2 wickets. At the resumption of play, Team 1 is given 8 overs to complete their innings. Team 1's final run score is 170. Team 1 completed 42 overs in total, so that's how many overs Team 2 has too. Using the Duckworth Lewis algorithm in our calculator, you would:

1. Select Team 1's innings interrupted from the "Interruption" option.
2. Optionally adjust the average score value of G50, but we will leave it at 245 for this example.
3. Enter 50 in the "Overs available" row.
4. Input 16 into the "Overs remaining at interruption" variable.
5. Enter 2 for the number of wickets lost.
6. Input 8 as the number of overs that remain after the interruption.
7. Enter the number of runs Team 1 scored, 170.
8. In the Team 2 section, enter 42 overs available. The calculator tells you that Team 2's target is 197 to win.
9. Again, enter the number of runs Team 2 actually scored to see how much they won or lost the match by.

To calculate this result manually, we find the resource percentages for each team. Team 2 has 42 overs left and has lost no wickets, so their resources are 91.7% from the table. For Team 1, their resources before the interruption are given by looking up 16 overs remaining and 2 wickets lost, which is 44.7%. At the resumption of play, they have 8 overs remaining and still have lost 2 wickets, which is 25.5%. Team 1's resources used is, therefore:

100% - 44.7% + 25.5% = 80.8%

Because Team 2 has more resources than Team 1, we need to increase the target to win to compensate, so we use the equation:

Team 2's par score = S + G50 × (R2 - R1)/100 = 170 + 245 × (91.7 - 80.8)/100 = 196.71

Assuming that the second innings is delayed by 20 overs, and the first team scored 240 runs in 50 overs, follow these steps to calculate the target:

1. Assess how many overs are available for the second team:
   50 - 20 = 30 overs.

2. Look up the DLS resources table. The second team has 30 overs and 10 wickets, which gives us 75.1% available resources.

3. Use this data in the standard edition of the DLS method:
   Team 2 target = 240 × 75.1/100 = 180.24.

4. Round it to get the second team's target:
   181 runs.

In an ODI match, both teams must've faced at least 20 overs for the DLS method to be applicable unless one or both teams were bowled out earlier or the second team chased the score in less than 20 overs.

The DLS method asserts that each team has two primary resources to score runs:

1. The number of overs available.
2. The number of wickets left.

The most common methods used to resolve rain delays in limited overs cricket before the Duckworth-Lewis method were the average run rate and the most productive overs methods. Both these methods had intrinsic flaws - they ignored the wickets at hand and disregarded other factors. Using these methods often produced results that ultimately tipped the game's balance.