Last updated: Nov 27, 2024

Water Viscosity Calculator

Q: What is viscosity?

Viscosity is the measure of a fluid's resistance to flow . The higher the viscosity of a fluid is, the slower it flows over a surface. For example, maple syrup and honey are liquids with high viscosities as they flow slowly. In comparison, liquids like water and alcohol have low viscosities as they flow very freely.

Q: What is the unit of viscosity?

We can express dynamic viscosity in millipascals⋅second ( mPa⋅s ) or centipoise ( cP ) where 1 mPa⋅s = 1 cP . On the other hand, we can express kinematic viscosity in square millimeters per second ( mm²/s ) or centistokes ( cSt ) where 1 mm²/s = 1 cSt .

Q: What is the viscosity of water?

The viscosity of water is 1.0016 mPa⋅s at 20 °C . That is for its dynamic viscosity. Water viscosity varies depending on its temperature, and the higher the temperature is, the less viscous water is. Water's viscosity at, let's say, 80 °C is 0.354 mPa·s .

Q: Does temperature affect water viscosity?

Yes, water viscosity changes with temperature . Water tends to have higher viscosity at lower temperatures and a lower viscosity at higher temperatures. Think of placing water in a freezer. The water molecules at a lower temperature start to lose their energy, get attracted to each other more, and flows rather slowly until the water turns to ice.

Q: Do gases have viscosity?

Yes, gases have viscosity too . However, unlike with liquids, the temperature affects the viscosity of gases so that at higher temperatures, the viscosity of gases goes high, too. In other words, as it gets hotter, gases like air feel a bit stagnant than when it is colder.

Q: How do I convert kinematic viscosity to dynamic viscosity?

Simply multiply the kinematic viscosity of the liquid at a particular temperature by its density at that same temperature . For example, the kinematic viscosity and density of water at 78 °C is around 0.37344 mm² per second and 0.973 grams per cm³ , respectively. Multiplying them together, we get 0.37344 mm²/s × 0.973 g/cm³= 0.36336 mPa·s , which is the dynamic viscosity of water at 78 °C .

Q: What is the kinematic viscosity of water?

Around 1 mm² per second . At 20 °C , water's kinematic viscosity is around 1 mm² per second and goes higher at lower temperatures. At 10 °C , water's kinematic viscosity is around 1.3 mm² per second while at 30 °C , it goes to around 0.8 mm² per second . Increasing the temperature decreases the viscosity of water.

Q: Does water have a low viscosity?

Water has a low viscosity since water can flow readily. On the other hand, fluids that take time to flow, like honey and glycerol, have high viscosities. It is also worth noting that the temperature also affects the viscosity of fluids. Cold honey will flow even slower than honey at room temperature. In contrast, warm honey will flow faster than usual. This is also true with water.

Created by Kenneth Alambra

Kenneth Alambra

Holds a Bachelor’s degree in Civil Engineering with 3+ years experience in fit-out construction and another 3+ years in technical sales. Ken has always been interested in creativity and innovation. He finds himself having fun solving problems and thinking of ways to improve anything he comes in contact with. During his free time, he plays a lot of bullet chess, listens to some pop music, or tries to learn something new – like preparing his favorite foods. See full profile

Check our editorial policy

Reviewed by Dominik Czernia, PhD

Dominik Czernia

PhD, Institute of Nuclear Physics PAN

LinkedInWebsiteResearch Gate

Physicist at the Institute of Nuclear Physics in Kraków interested in magnetism and always ready to explain everything to everyone in simple terms. He is currently working on adding more scientific papers to his collection, accompanied by his son and another baby on its way. A perfectionist with an acute eye for detail, he has a unit converter in his brain and uses it to compare prices at the supermarket. Loves peace and quiet, especially during hiking. See full profile

Check our editorial policy

and Jack Bowater

New

Table of contents

What is viscosity?What is the viscosity of water?How to use our water viscosity calculator?How to calculate the viscosity of water?How to calculate the kinematic viscosity of water?FAQs

This water viscosity calculator will help you determine the viscosity of water at room temperature or any temperature, even those above $300\ \mathrm{\degree C}$ ! In this calculator, you will learn what the absolute viscosity of water is (commonly known as its dynamic viscosity) and how to convert it to kinematic viscosity. You will also learn how to calculate the viscosity of water and the effect of temperature on the viscosity of water using various methods.

This water viscosity calculator provides you with a water viscosity to temperature chart and table so you can reference the effects that temperature has on water's viscosity and density of water. Although our charts and tables are in SI units, in this calculator, you will also learn how we can express the viscosity of water in English units. Keep on reading to learn more!

What is viscosity?

Viscosity is the measure of a fluid's resistance to flow. The higher the viscosity of a fluid (liquid or gas), the slower it traverses across a surface. Imagine dripping maple syrup on your waffles for your breakfast. Maple syrup, a very viscous fluid, would pour slower than when you pour milk on your cereal as milk's viscosity is much lower. We can also express viscosity as the internal friction of a fluid in motion. The attraction between the molecules of a viscous fluid is much higher than that of a less viscous fluid.

"Image of pouring maple syrup onto a waffle and of milk onto a bowl of cereal."

However, when we apply heat or additional thermal energy to our fluids, their molecules start moving faster. As a result, in gases, molecules experience more friction against each other, making them flow slower and become viscous. In liquids, when molecules start to move faster, their attraction from each other weakens. This weakening results in liquid molecules to move more freely and, therefore, with a lower viscosity.

In this article, we'll focus more on the viscosity of liquids, specifically on the kinematic viscosity and the dynamic viscosity of water. When dealing with viscosities, when we mention "viscosity," we actually mean dynamic viscosity. Dynamic viscosity, or the absolute viscosity of water, or any fluid, is proportional to the tangential shear stress per unit area needed to move one plate at a constant speed over another plate at a maintained fluid thickness between these two plates, like in a Couette flow, as shown below:

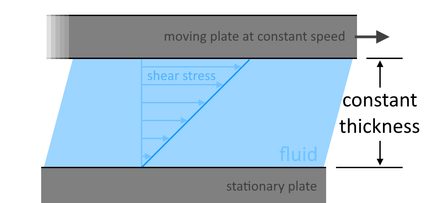
Cross-sectional illustration or a water layer showing the tangential force needed to move a specific area of water.

The larger the force or stress needed to move the plate, the more viscous the fluid is. When choosing between the two viscosities, it is worth noting that dynamic viscosity tells us about the force required to move the fluid at a certain speed. On the other hand, the kinematic viscosity tells about the speed the fluid reaches when a particular force is applied to the fluid.

We can measure dynamic viscosity in millipascals-second ( $\mathrm{mPa\cdot s}$ ) or with a fancier equivalent called the "centipoise." On the other hand, we can express kinematic viscosity in square millimeters per second ( $\mathrm{mm^2/s}$ ), which also has an equivalent unit called "centistokes." For the simplicity of this text, we will only be using milliPascals-second and square millimeters per second for dynamic viscosity and kinematic viscosity, respectively.

However, if you need to express the viscosity of water in English units, you can always convert the milliPascal part to pound-force per square foot, and the square millimeters to square inches, for the dynamic viscosity and kinematic viscosity respectively. You can use our pressure converter and area converter for these procedures, especially if you have a lot of values to convert.

What is the viscosity of water?

Water, being the most studied liquid, is the best fluid to start with when learning about viscosity. The dynamic viscosity of water at room temperature has a value of around $1.0\ \mathrm{mPa\cdot s}$ , and it decreases as temperature increases. This value is the viscosity of water at $20\ \mathrm{\degree C}$ . Below is a water viscosity to temperature chart that shows the effect of temperature on the dynamic viscosity and kinematic viscosity of water.

Water viscosity temperature chart that displays the dynamic and kinematic viscosities as well as the density of water at temperatures ranging from 0 °C to 370 °C.

The water viscosity to temperature chart above is a visual representation of the data recorded below. Experiments have been made at different temperatures to obtain this data. In the table below, we have also included water density since it has a crucial role in converting dynamic viscosity to kinematic viscosity (something we learned to do at the Poise-Stokes converter), as you will see in the next section of this text.

Temperature ( $\degree\mathrm{C}$ )	Dynamic viscosity ( $\mathrm{mPa\cdot s}$ )	Kinematic viscosity ( $\mathrm{mm^2/s}$ )	Fluid density ( $\mathrm{g/cm^3}$ )
$0$	$1.7880$	$1.7890$	$0.9999$
$1$	$1.7308$	$1.7313$	$0.9999$
$2$	$1.6735$	$1.6736$	$0.9999$
$3$	$1.6190$	$1.6191$	$1.0000$
$4$	$1.5673$	$1.5674$	$1.0000$
$5$	$1.5182$	$1.5182$	$1.0000$
$6$	$1.4715$	$1.4716$	$0.9999$
$7$	$1.4271$	$1.4272$	$0.9999$
$8$	$1.3847$	$1.3849$	$0.9999$
$9$	$1.3444$	$1.3447$	$0.9998$
$10$	$1.3059$	$1.3063$	$0.9997$
$20$	$1.0016$	$1.0034$	$0.9982$
$30$	$0.7972$	$0.8007$	$0.9956$
$40$	$0.6527$	$0.6579$	$0.9922$
$50$	$0.5465$	$0.5531$	$0.9880$
$60$	$0.4660$	$0.4740$	$0.9832$
$70$	$0.4035$	$0.4127$	$0.9778$
$80$	$0.3540$	$0.3643$	$0.9718$
$90$	$0.3149$	$0.3260$	$0.9653$
$100$	$0.2825$	$0.2950$	$0.9584$

How to use our water viscosity calculator?

To use our calculator, input the temperature that you want to know the water viscosities for. You can also mouse-over (for computers) or drag-over (for mobile phones) the chart in our calculator to see the viscosity values at any temperature.

We also included in our water viscosity calculator the water density values at any temperature as a bonus.

How to calculate the viscosity of water?

To determine the viscosity of water at any temperature, we can use the table or the water viscosity to temperature chart provided in the Effect of temperature on viscosity of water section of this text and use the interpolation method (for example the one we met at the linear interpolation calculator) for other temperatures not written in the table. Using the chart, we can approximate the temperature we want and then (1) draw a vertical line from the x-axis until it intersects the curve. By (2) drawing a horizontal line from this intersection, we can now see the approximate water viscosity at a particular temperature, like with the one shown below for $125\ \mathrm{\degree C}$ :

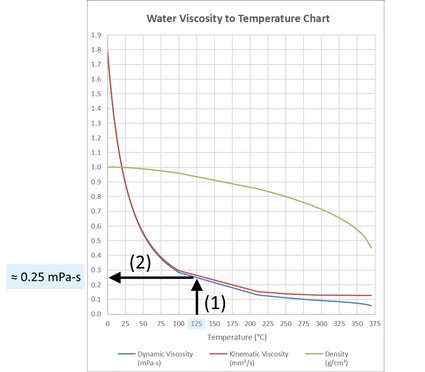
Image showing how to approximate the water viscosity by drawing a vertical line from the x-axis up to the line in the graph and drawing a horizontal line from this point towards the y-axis.

Depending on the method you decide to choose (use the water viscosity calculator with interpolation method or draw lines), you can get the values for water viscosity (dynamic and kinematic).

However, it is then a good practice to choose only one method when comparing multiple viscosity values at different temperatures. This way, the concepts behind the values you get will be consistent and appropriate for comparisons. Anyway, we'd choose the first method (the interpolation method) because it is more accurate than drawing vertical and horizontal lines over a chart.

How to calculate the kinematic viscosity of water?

Aside from calculating the dynamic viscosity of water, we may also need to determine the kinematic viscosity of water at any temperature. We can also use the water viscosity-temperature chart or table provided in this text and follow the same instructions given above. We can also calculate water's kinematic viscosity from dynamic viscosity by dividing the dynamic viscosity by water's density, as shown below:

\nu_T = \frac{\eta_T}{\rho_T}

where:

$\nu_T$ denotes the kinematic viscosity at temperature $T$ ;
$\eta_T$ – Dynamic viscosity at temperature $T$ ; and
$\rho_T$ – Density of water at temperature $T$ .

Please note that temperature also affects the density of water and that all necessary linear interpolation should be done prior to calculation. Let's say we have previously calculated the density of water at $78\ \mathrm{\degree C}$ to be approximately equal to $0.973\ \mathrm{g/cm^3}$ . Also, using the interpolation method, we find the dynamic viscosity of water at $78\ \mathrm{\degree C}$ to be around $0.36336\ \mathrm{mPa \cdot s}$ . We then convert this value of dynamic viscosity to kinematic viscosity as follows:

\begin{split} \nu_{78\ \mathrm{\degree C}} &=\frac{\eta_{78\ \mathrm{\degree C}}}{\rho_{78\ \mathrm{\degree C}}}\\[1.3em] &=\frac{0.36336\ \mathrm{mPa \cdot s}}{0.973\ \mathrm{g/cm^3}}\\[1.3em] &= 0.3734429599\ \mathrm{mm^2/s} \\[.5em] &\approx 0.37344\ \mathrm{mm^2/s}\\ \end{split}

Using the conversion method shown above, we can now say that water's kinematic viscosity at $78\ \mathrm{\degree C}$ is approximately $0.37344\ \mathrm{mm^2/s}$ .

FAQs

What is viscosity?

Viscosity is the measure of a fluid's resistance to flow. The higher the viscosity of a fluid is, the slower it flows over a surface. For example, maple syrup and honey are liquids with high viscosities as they flow slowly. In comparison, liquids like water and alcohol have low viscosities as they flow very freely.

What is the unit of viscosity?

We can express dynamic viscosity in millipascals⋅second (mPa⋅s) or centipoise (cP) where 1 mPa⋅s = 1 cP. On the other hand, we can express kinematic viscosity in square millimeters per second (mm²/s) or centistokes (cSt) where 1 mm²/s = 1 cSt.

What is the viscosity of water?

The viscosity of water is 1.0016 mPa⋅s at 20 °C. That is for its dynamic viscosity. Water viscosity varies depending on its temperature, and the higher the temperature is, the less viscous water is. Water's viscosity at, let's say, 80 °C is 0.354 mPa·s.

Does temperature affect water viscosity?

Yes, water viscosity changes with temperature. Water tends to have higher viscosity at lower temperatures and a lower viscosity at higher temperatures. Think of placing water in a freezer. The water molecules at a lower temperature start to lose their energy, get attracted to each other more, and flows rather slowly until the water turns to ice.

How do I determine the viscosity of water?

You can determine the viscosity of water at a particular temperature using the water viscosity-to-temperature chart or by the interpolation method using the water viscosity-to-temperature table. Using the chart, simply:

Find the temperature you need from the X-axis;
Draw a vertical line from the X-axis up until it reaches the graph of water viscosity;
At the intersection, draw a horizontal line going to the Y-axis to find the viscosity you are looking for.

Do gases have viscosity?

Yes, gases have viscosity too. However, unlike with liquids, the temperature affects the viscosity of gases so that at higher temperatures, the viscosity of gases goes high, too. In other words, as it gets hotter, gases like air feel a bit stagnant than when it is colder.

How do I convert kinematic viscosity to dynamic viscosity?

Simply multiply the kinematic viscosity of the liquid at a particular temperature by its density at that same temperature. For example, the kinematic viscosity and density of water at 78 °C is around 0.37344 mm² per second and 0.973 grams per cm³, respectively. Multiplying them together, we get 0.37344 mm²/s × 0.973 g/cm³= 0.36336 mPa·s, which is the dynamic viscosity of water at 78 °C.

How do I increase the viscosity of water?

Put the water at a very low temperature to increase its viscosity. At lower temperatures, water molecules tend to lose energy, making them pile up each other closely. This piling up results in the water molecules experiencing more friction against each other, making them flow slower or become viscous.

What is the kinematic viscosity of water?

Around 1 mm² per second. At 20 °C, water's kinematic viscosity is around 1 mm² per second and goes higher at lower temperatures. At 10 °C, water's kinematic viscosity is around 1.3 mm² per second while at 30 °C, it goes to around 0.8 mm² per second. Increasing the temperature decreases the viscosity of water.

Does water have a low viscosity?

Water has a low viscosity since water can flow readily. On the other hand, fluids that take time to flow, like honey and glycerol, have high viscosities. It is also worth noting that the temperature also affects the viscosity of fluids. Cold honey will flow even slower than honey at room temperature. In contrast, warm honey will flow faster than usual. This is also true with water.

How does sugar affect the viscosity of water?

Adding substances that make water thick, like sugar, increases the viscosity of water. The more sugar is added, the more viscous the water gets and the thicker it becomes. Adding heat to the mixture will help in mixing more sugar into the water. Once the mixture cools down to room temperature, the mixture will be more viscous than when it is still hot.

Does salt affect the viscosity of water?

Yes, adding salt to water increases the viscosity of water. Since adding salt to water makes a thicker and denser solution, its viscosity also increases. Though it might not be readily felt when comparing saltwater to freshwater, it will already be noticeable in higher salt concentrations.

How do I measure the viscosity of water?

You can use a viscometer. There are many types of viscometer, but one of the simplest and easiest to use is the Ostwald viscometer.

A ostwald viscometer is a U-shaped glass tube with designated bulbs and two markings wherein the liquid being tested should pass through. During the observation, the time it takes for the liquid level to pass through the two markings will represent the liquid's kinematic viscosity. This procedure must be done at a known temperature.