Mass Moment of Inertia Calculator

The cylinder mass moment of inertia calculator is a powerful tool that will answer the following famous question: Which toilet paper runs faster on an inclined plane; a new toilet paper or the almost empty one? Or maybe you were always curious, why heavier, solid bodies rotate faster than hollow lighter bodies? Well, stay tuned because this will be a DIY (do it yourself) experiment that will explain all these and more.

The purpose of the cylinder mass moment of inertia calculator is to demonstrate how the mass and shape of a cylinder affect its racing time if we put a body at the top of an inclined plane. In this case, we will consider three main cylindrical types:

• Solid cylinder;
• Cylindrical tube; and
• Cylindrical shell.

Then, because we will have cylinders rotating downwards, we will need to find the acceleration to obtain the racing time. But first...

In short, the mass moment of inertia is the resistance that a body has to start having an angular acceleration. In more simple words, it is the resistance a body has against starting to rotate. Remember this: "The larger the moment of inertia, the more energy is required to start the rotation movement"

First, it is important to mention that we always define the mass moment of inertia along a rotation axis. In fact, we can have any rotation axis we can imagine; however, the most basic ones are X, Y, and Z. In the following lines, we will cover the cylinder mass moment of inertia formulas:

• 1) Solid Cylinder

Meanwhile, the formulas for each axis are:

• 2) Cylindrical tube

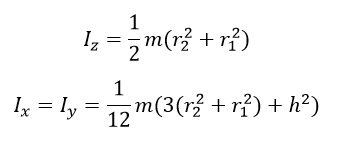
• 3) Cylindrical shell

For this experiment, we will use several bodies such as tapes, toilet paper, alcohol bottles, and make them rotate about their Z-axis.

Now, you might already be able to predict the results. If you give a quick check to the mass moment of inertia calculator and its equations, you will notice that given the same radius and mass, the cylindrical shell will have a bigger mass moment of inertia than the cylindrical tube and the solid cylinder. See:

Consequently, we will have that the cylindrical shell will need more time to cover the same distance than the other bodies. In other words, the empty toilet paper roll (cylindrical shell) will lose the race against a new one (cylindrical tube).

The next step is to find out how to relate mass moment of inertia with time, speed, and acceleration. Thankfully, Newton already explained how to relate the three later ones:

• $\rm{ a = 2 \times ( \Delta d - v_{i} \times \Delta t)/\Delta t^2}$

which for a non-existent initial speed $\rm{ v_{i} = 0}$, and by considering $\rm {\Delta d = L}$ as the distance covered:

$\rm {a = 2 \times L / \Delta t^2}$

and arranged for calculating time:

$\rm {\Delta t = \sqrt{2 \times L / a}}$

Then, we just need the link with the mass moment of inertia. As we remember for sliding movement on inclined planes, we have:

$\rm{a = F/m}$

where we divide the force accordingly to the inclination angle $\Theta$ for obtaining the force parallel to the inclined plane ($\rm{F_{i}}$) and the force perpendicular to the inclined plane:

$\rm{F_{i} = m \times g \times sin(\Theta)}$
$\rm{F_{n} = m \times g \times cos(\Theta)}$

Finally, after considering the conservation of energy law where the sum of the potential and kinetic energies equals the final mechanical energy, and also taking into consideration the rotational kinetic energy calculator $\rm{\Kappa}$equation:

$K = 0.5 \times I \times \omega ^ 2$

Where, $\rm{\omega}$ represents the angular velocity. Therefore, we have:

$\rm { a = F_{i} / (m + I/r^2)}$

So, as we can see, the acceleration is influenced by the moment of inertia. Thus, the racing time will be affected too.

For more useful information on energy, check out our related tools: the potential energy calculator and the kinetic energy calculator.

Once we covered all the formulas needed, we will proceed to the experiment. We will use an inclined plane, an alcohol bottle, new toilet paper, empty toilet paper, a metal can, and several tapes. The numbering we are considering is:

Here we can appreciate an upper view to show the difference in inner and outer radius.

First, we compared the alcohol bottle (assumed to be a solid cylinder) and the blue tape (taken as a cylindrical tube). The results were:

Starting point:

Ending point:

We can clearly see that the alcohol bottle won the race. It is as expected because the moment of inertia of a solid cylinder offers less resistance to its rotation than a cylindrical tube.

It is essential to point out that even though the alcohol bottle is heavier than the tape, it still offers less opposition to rotation because of its mass distribution, which is closer to the center than the tape. Then, we continue comparing the alcohol bottle against the metal can (cylindrical shell).

Starting point:

Ending point:

Of course, here, the difference is even more significant; again, because of the same reason: The geometry of a cylindrical shell offers more resistance to its rotation compared to a solid cylinder. The lower the mass moment of inertia, the higher acceleration; consequently, less racing time. For the next part, we compare the blue tape with the metal can.

Starting point:

End point:

Similar to what we defined before, a cylindrical tube will accelerate faster than a cylindrical shell because of its moment of inertia. Note that the metal can is undoubtedly lighter in mass; however, that does not overcome the effects of mass distribution on its moment of inertia. In the case of the tape, the mass is closer to the center of rotation.

For the next competition, we will have tapes #3 and #4.

Starting point:

Ending point:

We can notice that blue tape (tape #3) won again. We can suspect that the reason was that the blue tape has more tape compared to the mustard #4 tape. For verifying it, we will use our fantastic cylinder mass moment of inertia calculator.

For the blue tape:

$\rm{Inner\ radius = 3.75\ cm}$

$\rm{Outer\ radius = 5.45\ cm}$

$\rm{Mass (m) = 0.15\ kg}$

For the mustard tape:

$\rm{Inner\ radius = 3.75\ cm}$

$\rm{Outer\ radius = 4.7\ cm}$

$\rm{Mass (m) = 0.1\ kg}$

For the plane:

$\rm{Length (L) = 112\ cm}$

$\rm{Height (H) = 15.5\ cm}$

$\rm{Angle (\Theta) = 7.95 ^{\circ}}$

After applying the cylinder mass moment of inertia equation, we obtain:

For the blue tape:

$\rm{Moment \ of \ inertia = 0.00032824 kg \times m^2}$

$\rm{Rolling \ time (t) = 1.694\ s}$

For the mustard tape:

$\rm{Moment \ of \ inertia = 0.00018076 kg \times m^2}$

$\rm{Rolling \ time (t) = 1.7334\ s}$

Clearly, from these results, we can see that the blue tape (#3) won the race.

Finally, we will do the test to answer the initial question of the cylinder mass moment of inertia calculator: Which rolls faster: the empty toilet paper or the new one?

Considering that we can represent the new one as a cylindrical tube and the empty one as a cylindrical shell, we might already have the answer. Ready? Go!

Starting point:

Ending point:

As expected, the new one wins. So, remember, if you are in an emergency, be careful letting the new toilet paper fall on the floor because it will go away faster.

In conclusion, we would like to point out the next idea: The hollow body will always be the loser in the race, independently of its mass.