Mass Moment of Inertia Calculator
The mass moment of inertia calculator is a complex tool that helps estimate the moment of inertia of objects with different shapes. This physical quantity is otherwise known as angular mass or rotational inertia.
The moment of inertia is a characteristic property of a rigid body. It plays a similar role in the dynamics of rotational motion as the normal mass in the dynamics of translational motion. For example, the mass in the kinetic energy formula is replaced by the moment of inertia in the rotational energy equation (see rotational kinetic energy calculator).
You can use the mass moment of inertia calculator right now – just select a figure and enter its parameters. Or read on to learn what is the moment of inertia, what its units are, and how to calculate the moment of inertia. In the following text, we have also prepared a moment of inertia table with about 23 different figures. It contains almost all of the most common object shapes.
What is the moment of inertia? – moment of inertia units
Moment of inertia is the measure of the body's rotational inertia relative to a defined, fixed axis of rotation. It determines the torque that is needed for a desired angular acceleration (see torque calculator and angular acceleration calculator). It is just like how mass determines the force needed for a desired acceleration. In other words, the moment of inertia tells us how difficult it is to rotate an object around a specific axis. Remember that the choice of axis is very important; the final moment of inertia value might strongly depend on it!
The physical dimension of the moment of inertia is mass × length². The SI unit of the moment of inertia is kilogram meter squared kg·m², and the imperial or US units are pound-foot second squared lb·ft·s² or pound-foot squared lb·ft². With the mass moment of inertia calculator, you can perform calculations in any of those units you prefer.
Moment of inertia equation
The moment of inertia of a material point is the product of its mass and the square of the distance from the axis of rotation. It can be expressed with the following moment of inertia equation:
If you consider a body consisting of material points, then the total moment of inertia is simply the sum of their moments of inertia:
where:
- – Symbol of the summation, summing all components from to ;
- – Mass of 'th material point; and
- – Distance of 'th material point from the axis of rotation.
However, for bodies with a constant distribution of mass, the summation in the above formula becomes an integral:
where integration takes place over the entire volume of the body.
Although integration is not always an easy task, there are many ready-made formulas for the moment of inertia of specific solids. You can select the figure from the list in this mass moment of inertia calculator or check the moment of inertia table in the next section.
The mass moment of inertia of a body that we just described and the second moment of area are often confused. Remember that the mass moment of inertia units is kg·m² (lb·ft·s² or lb·ft²), while the second moment of area units is m⁴ (ft⁴).
💡 Learn more about the second moment of area with our moment of inertia calculator.
Moment of inertia table
You have already learned what the moment of inertia is and how you can calculate it from its definition. The table below lists moment of inertia equations for simple objects with a constant mass density that you can select in our mass moment of inertia calculator. When calculating moments of inertia, it is sometimes useful to exploit the parallel axis and perpendicular axis theorems to estimate moments of inertia about different axes.
Data and figures from .
No. | Figure and moments of inertia |
|---|---|
#1 - Ball. Solid ball of radius r and mass m with axis of rotation going through its center. | 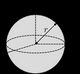 |
 | |
#2 - Circular hoop. Thin circular hoop of radius r and mass m with three axes of rotation going through its center: parallel to the x, y or z axes. |  |
 | |
 | |
#3 - Cuboid. Solid cuboid of length l, width w, height h and mass m with four axes of rotation going through its center: parallel to the length l, width w, height h or to the longest diagonal d. |  |
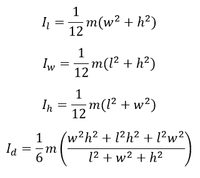 | |
#4 - Cylinder. Solid cylinder of radius r, height h and mass m with three axes of rotation going through its center: parallel to x, y and z axes. |  |
 | |
 | |
#5 - Cylindrical tube. Cylindrical tube of inner radius r₁, outer radius r₂, height h and mass m with three axes of rotation going through its center: parallel to x, y and z axes. |  |
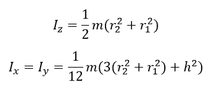 | |
#6 - Cylindrical shell. Cylindrical shell of radius r and mass m with axis of rotation going through its center, parallel to the height. | 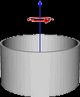 |
 | |
#7 - Disk. Thin solid disk of radius r and mass m with three axes of rotation going through its center: parallel to the x, y or z axes. | 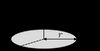 |
 | |
 | |
#8 - Dodecahedron. Solid and hollow, regular dodecahedron (twelve flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. |  |
 | |
 | |
where: | |
 | |
#9 - Ellipsoid. Solid ellipsoid of semiaxes a, b, c, and mass m with three axes of rotation going through its center: parallel to the a, b, or c semiaxes. |  |
 | |
 | |
 | |
#10 - Icosahedron. Solid and hollow, regular icosahedron (twenty flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. |  |
 | |
 | |
where: | |
 | |
#11 - Isosceles triangle. An isosceles triangle of mass m, vertex angle 2β, and common-side length L with axis of rotation through tip, perpendicular to plane. | 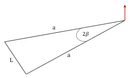 |
 | |
#12 - Octahedron. Solid and hollow, regular octahedron (eight flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. | 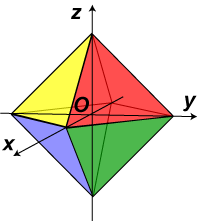 |
 | |
 | |
#13 - Point mass. Point mass m at a distance r from the axis of rotation. | 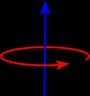 |
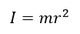 | |
#14 - Rectangular plate. Thin rectangular plate of length l, width w, and mass m with axis of rotation going through its center, perpendicular to the plane. |  |
 | |
#15 - Regular polygon. Plane regular polygon with n vertices, radius of the circumscribed circle R, and mass m with axis of rotation passing through its center, perpendicular to the plane. Radius R can be expressed with side s. |  |
 | |
 | |
#16 - Right circular cone (hollow). Hollow right circular cone of radius r, height h, and mass m with three axes of rotation passing through its center: parallel to the x, y, or z axes. |  |
 | |
 | |
#17 - Right circular cone (solid). Solid right circular cone of radius r, height h, and mass m with three axes of rotation passing through its center: parallel to the x, y, or z axes. | 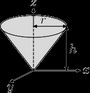 |
 | |
 | |
#18 - Rod. Rod of length L and mass m with two axes of rotation: about its center and one end. | 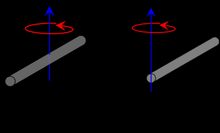 |
#19 - Sphere. Hollow sphere of radius r and mass m with axis of rotation going through its center. |  |
 | |
#20 - Spherical shell. Spherical shell of inner radius r₁, outer radius r₂, and mass m with axis of rotation going through its center. |  |
 | |
#21 - Tetrahedron. Solid and hollow, regular tetrahedron (four flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. | 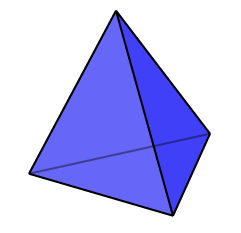 |
 | |
 | |
#22 - Torus. Torus with minor radius a, major radius b and mass m with axes of rotating going through its center: perpendicular to the major diameter and parallel to the major diameter. | 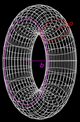 |
 | |
#23 - Two point masses. Two point masses m₁ and m₂, with reduced mass μ, separated by a distance r with axis of rotation going through the center of mass and perpendicular to the line joining the two particles. |  |
 |
FAQs
How can I calculate the moment of inertia?
Generally, to calculate the moment of inertia:
- Measure the masses (mi) and distances (ri) from the axis of rotation.
- Multiply the mass of each particle in the body by the square of its distance from the axis of rotation: miri2.
- Sum all the products of the particle's mass with the square of its distance:
I = ∑ miri2.
What is the unit of the moment of inertia?
The SI unit of the moment of inertia is kg⋅m2. The formula for a moment of inertia is mr2 when the unit of m (mass) is kg, and the unit of r (distance) is m. The imperial or US unit for the moment of inertia is lb·ft·s2.
What does the moment of inertia depend on?
The moment of inertia mostly depends on the position and orientation of the axis of rotation. Other parameters are the figure's size and shape, as well as the distribution of weight around a given axis.
What is the moment of inertia of a spinning sphere?
2.94 kg⋅m2 or 2.1684 lb·ft·s2, assuming that the sphere has a mass of 9 kg and a radius of 0.7 m.
- Use the moment of inertia formula for a sphere: I = 2/3mr2.
- Enter the mass of 9 kg and radius of 0.7 m:
I = 2/3 × 9 kg × (0.7 m)2 = 2.94 kg⋅m2.
What is the moment of inertia of the particle system?
The moment of inertia for a point particle is equal to mr2, so for a system of equal particles will be I = m ∑ ri2. For example, if you have a system of 3 particles with masses of 0.2 kg and distances of 0.1, 0.3, and 0.5 m from the axis of rotation, the total moment of inertia will be I = 0.2 ∑ [ 0.12 + 0.32 + 0.52] = 0.07 kg⋅m2.
Can the moment of inertia be negative?
No, the moment of inertia always has positive values. The moment of inertia is the product of mass and distance from the axis of rotation squared. Mass cannot be negative, and the square of any real number is also positive, so the product is always positive.