Slenderness Ratio Calculator

The slenderness ratio calculator is a tool that instantly helps you determine the slenderness ratio of a column of any length and for different cross-sectional areas.

In the field of structural engineering, the term slenderness ratio is used as a factor to identify the tendency of a column to fail by buckling. This type of failure is primarily associated with long and thin elements, mainly columns.

If you're interested in learning more about this subject, we invite you to keep reading and also find:

• The slenderness ratio formula;
• How to calculate the slenderness ratio of a column; and
• The limits of the slenderness ratio.

Related to this topic, we have a buckling calculator with which you can determine the critical load of a column 🚧

The slenderness ratio (KL/r) is a factor that indicates the tendency of a column to buckle. The higher the value, the easier it's for it to buckle. Columns under compressive loads can fail either by yielding, buckling, or a combination of these two. In the case of thin and long columns, the first mode of failure will be by elastic buckling.

The slenderness ratio formula is given by the expression:

λ = Leff / r = K × L / r

where:

• λ — Slenderness ratio;
• Leff — Effective length;
• r — Radius of gyration;
• K — Effective length factor; and
• L — Length of the column.

For example, a column of Leff = 8.0 m and r = 28.87 mm:

λ = 8.0 m / 28.87 mm = 277.1

The effective length Leff represents the longitude between the inflection points in the buckled column.

The slenderness ratio comes from Euler's equation for columns:

This equation gives the critical load $P_\text{cr}$, which is the load at which a slender column will buckle. Columns under this load are subjected to unstable equilibrium.

For loads below, the column will remain straight. Loads equal to $P_\text{cr}$ will not cause lateral deflection. Loads greater than the critical load will make the column deflect laterally and collapse.

We can continue by dividing the previous equation by the cross-sectional area of the column to express the critical axial stress ($\sigma_\text{cr}$):

where:

• $E$ — Young's modulus of the material;
• $I$ — Moment of inertia around the weak axis; and
• $A$ — Cross-sectional area of the column. You can read how to calculate the cross-sectional area in our cross-sectional area calculator.

Since the radius of gyration, $r$ is given by:

We can express the stress formula as:

where the term $KL/r$ represents the slenderness ratio.

From the above, it is possible to tell that we can determine the slenderness ratio in terms of its geometrical characteristics.

In order to calculate the slenderness ratio of a column, follow these steps:

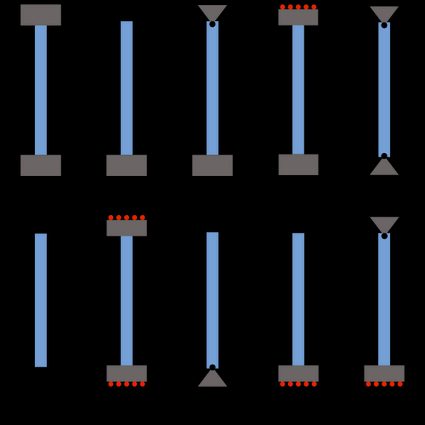
1. Define the end conditions. This will have an effective length factor K associated.

2. Calculate the effective length as:

   Leff = K × L

3. Continue to determine the radius of gyration r according to the cross-section of the column:

   r = √(I / A)

   where:

   • r — Least radius of gyration;
   • I — Moment of inertia around the weak axis; and
   • A — Cross-sectional area of the column.

4. Finally, with Leff and r, proceed to calculate the slenderness ratio λ:

   λ = Leff / r

The axis with the least moment of inertia and radius of gyration becomes the neutral bending axis when buckling occurs.

If you're unsure about how to determine the second moment of inertia of common shapes, then we recommend taking a look at our moment of inertia calculator to master this subject 😎

The slenderness ratio allows classifying columns as short, medium, or long. For long columns, Euler's formula gives a good approximation. Whilst, for intermediate and short columns, we should use Johnson's empirical parabolic formula instead. The transition point between these two occurs at the critical slenderness ratio.

The critical slenderness ratio definition is given as follows:

This expression relates to the material's properties, Young's modulus of elasticity $E$, and its yield stress $\sigma_y$.

The critical slenderness ratio allows defining the slenderness ratio limits, which help classify and identify columns as long, intermediate, or short.

For structural steel A36, the limits for the slenderness ratio are:

• For short columns:

  40 ≤ (KL/r)

• For intermediate columns:

  40 < (KL/r) < 120

• For long columns:

  120 ≤ (KL/r) ≤ 200

For aluminum:

• The limits for slenderness ratio of short columns:

  0 ≤ (KL/r) ≤ 12

• Intermediate columns:

  12 < (KL/r) < 55

• Limit slenderness ratio for long columns:

  55 ≤ (KL/r)

For wooded columns, the limits for the slenderness ratio are:

• Short columns:

  0 ≤ (KL/d) ≤ 11

• Intermediate columns:

  11 < (KL/d) ≤ 26

• Long columns:

  26 < (KL/d) ≤ 50

The slenderness ratio calculator is a tool that will quickly help you determine the slenderness ratio of a column of any length and for different cross-sectional shapes. To use this tool:

1. Begin by entering the column's dimensions that you'd like to evaluate and determine its slenderness ratio.

2. In the Length (L) field, enter the respective length dimension of the column.

3. Below, you'll find a dropdown menu (End conditions) from where you'll be able to select the boundary conditions of the column.

4. On the next row, Column section shape, you can select the cross-sectional shape of the column. Choose the shape that you are interested in evaluating.

5. Enter the respective dimensions of the cross-section.

   For example, if you choose a rectangular cross-section, the calculator will ask you to provide the rectangle's Height (h) and Base (b) dimensions. For other shapes, the calculator will request specific dimensions accordingly.

6. That's it! Once you've input this information, the calculator will give you the slenderness ratio λ for the given set of dimensions.