Buckling Calculator

This buckling calculator helps you estimate the behavior of a column under axial loads. The calculator determines the critical load value based on Euler's formula for columns. Buckling occurs when a column is under high compressive load, and it is observable before the stress reaches the yield stress value in the column, making the phenomenon catastrophic.

Columns are a load-bearing member, be it the concrete columns for your house or the desk where you have set up your 3D printer! They can fail suddenly if the buckling load goes beyond the critical load. For instance, it could be the excessive snow load on the roof due to rough weather! Therefore, engineers need to understand this concept to design components considering the buckling loads. To this end, we hope the article below will help you get started on how to calculate buckling load.

Buckling is a phenomenon under which a member can suddenly fail due to excessive compressive load. The load at which the member fails is known as the critical load, $F_{crit}$ or $F$. The buckling causes a reduction in the axial stiffness of the column that results in displacement and rotations having catastrophic consequences.

The buckling in a column depends on the elastic stiffness of the material rather than its load-bearing compressive strength. That is why the buckling load requires a separate consideration in the design and the stresses, as the failure due to buckling could occur before the stresses in the column satisfy the yield criterion.

The buckling induces instabilities in the structure causing it to fail. The buckling can be due to flexural or torsional loads and is categorized as flexural and torsional buckling. There's also a mixed case in which the combination of flexural and torsional load causes the structure to buckle, known as flexural-torsional buckling.

Euler's buckling formula helps estimate the critical load. However, that formula is applicable to only long columns. For short columns, you need to use Johnson's formula. So how do we know if the column is long or short? — We check for the slenderness ratio. It should be less than the critical slenderness ratio. You can read more about concrete columns in our concrete column calculator.

The slenderness ratio $S$, in simple terms, is a means to define the aspect ratio of a column or a building. The more slender the object larger the reinforcement it needs to dampen its vibration and swinging. It is the ratio of the effective length of the column, $L_{e}$, and the least radius of gyration, $R$.

The radius of gyration is the square root of the ratio of an area moment of inertia, $I$ and cross sectional area, $A$. Mathematically, this is:

Visit our moment of inertia calculator and cross sectional area calculator to know more. Further, the critical slenderness ratio, $S_{crit}$, is a function of yield stress, $\sigma_y$, and Young's modulus, $E$. Such that:

The column buckling calculator first calculates the slenderness ratio and compares it with the critical slenderness ratio, $S_{crit}$. If the slenderness ratio is lesser than its critical counterpart, the we classify the column as a short column. They are more prone to fail due to compression and without much buckling. Therefore, Johnson's formula is used to calculate the load in such cases. Johnson's formula for the short columns is:

Suppose the slenderness ratio is larger than the critical slenderness ratio. In that case, the column is considered a long one, and you must use Euler's column buckling equation to calculate the critical buckling load for the said column.

The column buckling equation gives the critical load for buckling to occur in a column. For a column having an effective length $L_e$, the second moment of inertia, $I$, and material's Young's modulus, $E$, the buckling load, $F$, is given by the equation:

The effective length, $L_e$, is a function of the measured length of the column, $L$, and the Effective length factor, $K$. The effective length factor is obtained using the boundary conditions applied to the column. The table below mentions the value of the K factor.

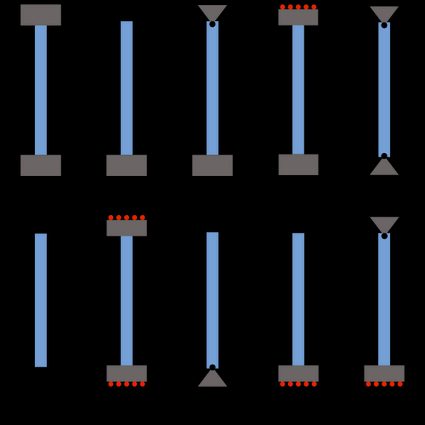
Each boundary condition has different restrictions on the associated degrees of freedom at the top and bottom end of the column. Use the following table if you get confused among these. Considering the displacement along $1, 2,$ and $3$ — directions as $\text{U}_1, \text{U}_2, \text{U}_3$ and the rotations as $\text{UR}_1, \text{UR}_2, \text{UR}_3$. The 0 implies the degree of freedom is restricted, whereas — means the degree of freedom is free.

Let's find out the critical buckling load for the column with the following properties:

• Boundary conditions: Free-Free
• Area moment of inertia: $100 \text{ mm}^4$
• Area of cross section: $1.2 \text{ mm}^2$
• Length of the column: $1 \text{ m}$
• Material: Al6061-O

To find the buckling load:

1. Select the boundary condition as Free-Free.
2. Enter the area moment of inertia as $100 \text{ mm}^4$.
3. Insert the area of cross-section as $1.2 \text{ mm}^2$.
4. The calculator returns the radius of gyration:

5. Fill in the length of column as $1 \text{ m}$.
6. The calculator determines the effective length as $1.2 \text{ m}$.
7. Select the material as Al6061-O to get the properties such as Young's modulus and yield stress.
8. The calculator now checks for slenderness ratio to classify the column:

9. The slenderness ratio is greater than the critical value, therefore, the buckling calculator determines the Euler's critical load: