Resonant Frequency Calculator

If you would like to calculate the resonant frequency of an LC circuit, look no further — this resonant frequency calculator is the tool for you. Enter the inductance and capacitance and in no time at all you'll find the resonant and angular frequency. We also provide some theory as it may be handy — below you'll find out how to calculate resonant frequency as well as a short definition about what the resonant frequency actually is.

If you're interested in electronic circuits, you would probably like to know how to obtain some fraction of input voltage — our voltage divider calculator is a must for that task.

An LC circuit (also called a resonant circuit, tank circuit, or tuned circuit) is an idealized RLC circuit of zero resistance. If you are looking for the "non-ideal" circuit, head to our RLC circuit calculator!

An LC circuit contains only an inductor and a capacitor, in a parallel or series configuration:

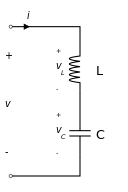
Tank circuits are commonly used as signal generators and bandpass filters — meaning that they're selecting a signal at a particular frequency from a more complex signal. They are widely applied in electronics — you can find LC circuits in amplifiers, oscillators, tuners, radio transmitters and receivers. LC and RC circuits can be used to filter a signal by blocking certain frequencies.

The resonant frequency is a natural, undamped frequency of a system. If we apply a resonant frequency, the oscillations become the maximum amplitude, and even relatively small forces can produce large amplitudes. However, if any other frequency is chosen, that signal is dampened.

There are many different types of resonances, e.g.:

• Mechanical and acoustic;
• Electrical;
• Optical;
• Orbital; and
• Molecular.

For LC circuits, the resonant frequency is determined by the capacitance C and the impedance L.

To calculate the resonant frequency of a circuit composed of an inductor and a capacitor, follow these steps:

1. Write down the capacitance C in farads.
2. Write down the inductance L in henries.
3. Input both parameters in the resonant frequency formula: f = 1 / (2π × √(L × C)).

where:

• $f$ — The resonant frequency;
• $L$ — The circuit inductance; and
• $C$ — The circuit capacitance.

Where does this formula come from? Resonance in the LC circuit appears when the inductive reactance of the inductor becomes equal to the capacitive reactance of the capacitor. So:

Then, after transforming the equation, we find:

So:

And finally:

Also, the angular frequency may be calculated from the following, well-known formula:

Using our tool is a walk in the park:

1. Enter the capacitor value. For example, our capacitance is equal to $1\ \mathrm{μF}$.
2. Type the inductance. Our inductor in our LC circuit equals $0.18\ \mathrm{mH}$.
3. The resonant frequency calculator did the job! We quickly found out what the resonant frequency is: 11.863 kHz. You can also check the angular frequency as well, as the value will appear underneath.

A resonant frequency calculator is a flexible tool, so — as usual — you can type any two variables, and the missing one will be calculated in a flash.