Open Channel Flow Calculator

This open channel flow calculator will help you find water flow velocity and volumetric flow rate through an open channel, given the channel's roughness coefficient, slope, and cross-sectional area.

In this calculator, you will learn how Manning's equation works and how to use it to determine water flow. You will also learn about the most efficient cross-sections of open channels. Keep reading to start learning.

Transporting water from one place to another can be done in two ways – with the help of pressure or with the help of gravity. If we want to bring water up a building, we could do this with a powerful water pump. The water pump would push the water up the pipes by applying a large amount of pressure to the water through mechanical action, usually by centrifugal force. In this case, water will fill the pipes as it travels upwards. As the pipe cross-section is fully enclosed and not directly exposed to atmospheric pressure, this would be called a closed channel.

On the other hand, we call it an open channel flow when gravity acts in transporting the water, like in rivers or canals where the water flows from a higher to a lower elevation and the surface of the water is "open" or exposed to the atmospheric pressure. There are also some cases wherein water flows due to gravity, but the channel or pipe is filled. You can learn more about such cases in our pipe flow calculator.

In this open channel flow calculator, we dive into the simplest form of open channel flow and consider steady and uniform flow. In a steady uniform flow, the flow rate does not change throughout a channel that has uniform cross-sectional shape, slope, and roughness. In this kind of flow, we can then calculate the dimensions of the chosen uniform shape as long as we have all the other characteristics of the channel.

In the late 19th century, an accountant-turned-engineer named Robert Manning developed an equation that describes the effects of a channel's characteristics on an open channel's water flow rate. Manning's equation was developed to fit the data recorded during his time.

In his equation, Manning concluded that the water flow rate depends on the material used in constructing the channel, the channel's cross-sectional shape, and its slope.

The material used in the channel construction describes the roughness of the channel surface. The rougher the surface is, the slower the water flows through it. Lining a channel with a smooth-finish concrete or grouted rip rap would allow a faster flow of water compared to a natural channel. Rivers and other natural water streams are examples of natural channels usually lined with river rocks and some underwater vegetation.

The channel's shape also affects the water flow rate in important ways. First, the larger the cross-sectional area of the channel, the more water can flow through it. However, the water flow rate slows down due to friction between the water and the channel's surface. We can quantify this interface where the water meets the channel's surface by what we call the wetted perimeter.

The wetted perimeter is the cross-sectional length of the channel that the water touches (and gets wet), hence its name. The larger the wetted perimeter is, the more area the water gets in contact with the channel. That results in the slowing down of the water flow.

In open channel flow, the slope of the channel also affects the water flow rate. The steeper the slope of the channel is, the faster the water flows down the channel. Our elevation grade calculator can help you determine the slope of a particular area.

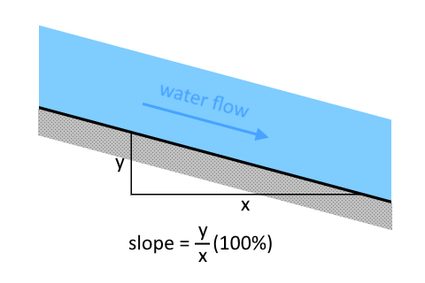
With these concepts in mind, Manning's formula is as follows:

where:

• $V$ – Velocity or water mass flow rate;
• $n$ – Manning's roughness coefficient;
• $R$ – The channel's hydraulic radius, calculated by dividing the water flow's cross-sectional area $A$ by its wetted perimeter $P$ (i.e., $R = \frac{A}{P}$); and
• $s$ – Slope of the channel's bottom surface.

Examining Manning's equation, we can see that the area and slope are directly proportional to the water flow rate, which means an increase in area and slope would increase the water flow rate. On the other hand, the roughness coefficient and the wetted perimeter are inversely proportional to the water flow rate, meaning that increasing their values would decrease the water flow rate.

Apart from this flow rate value, we can also consider the volumetric flow rate, which is simply the product of the mass flow rate and the cross-sectional area, as shown below:

where:

• $Q$ – Volumetric flow rate;
• $V$ – The calculated mass flow rate; and
• $A$ – Cross-sectional area of the water flow.

In the construction of large projects like water channels, we want to design these structures so that they are relatively easy to build while also being cost-efficient. Knowing the channel's characteristics and the potential water flow rate it needs to carry helps us know which channel cross-sections are most economical and efficient.

Basically, we want to have a cross-sectional area that is large enough to meet our flow rate requirements. At the same time, we have to minimize the wetted perimeter of our channel. To do this, we need the help of the mathematical concepts of minima and maxima, where we obtain derivatives of an equation and equate them to zero. We will not derive each of the equations here, but we have recorded the equations for each channel dimensions as shown in the table below in terms of the water flow depth, $y$:

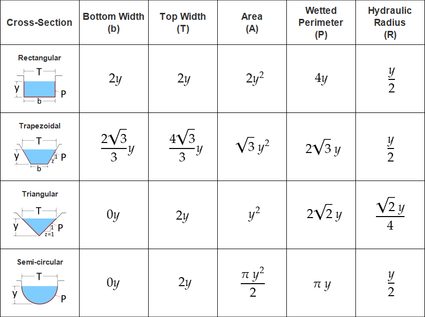
As some form of mnemonics, we can imagine a few things to understand the table above better. For the most efficient rectangular channel, imagine a square channel filled halfway. On the other hand, you can imagine a regular hexagon filled halfway for the most efficient trapezoidal channel. You can also imagine a half-filled square channel for the most efficient triangular channel. Only this time, the imaginary square channel must be tilted 45° to the side. Lastly, letting water flow at a depth equal to the radius of a circular pipe or a semi-circular channel results in another most efficient cross-section.

By arbitrarily setting the same value for the area of each cross-section, we can calculate their corresponding water flow depth values, $y$. By using these y values to solve for their corresponding wetted perimeters, it turns out that the semi-circular channel provides us with the smallest wetted perimeter value. We can then say that the semi-circular channel is the most economical channel of all the cross-sections.

However, although semi-circular channels would need the least materials to line a channel, they are actually the most difficult channel shape to build. If we consider the other cross-sectional shapes for a given area, the trapezoidal channel provides us with the next smallest value for the wetted perimeter. Trapezoidal channels are also easier to build than semi-circular channels, making them almost like the go-to cross-section for open channels nowadays.

You can use our open channel flow calculator to find the water flow rate for custom-sized channel designs and the most economic cross-sections. You may enter your desired values for the channel dimensions when using the custom design option in the design field. The calculator will then tell you the cross-sectional area of the water flow, the channel's wetted perimeter, its hydraulic radius, mass flow rate, and volumetric flow rate.

On the other hand, when selecting the most efficient design option, you can simply input the water flow depth. Once you choose the channel surface roughness coefficient and enter a channel slope, you will see the results. In this option, we've utilized the constants given in the table from the Most efficient cross-section of open channels part of this text to calculate efficient and economical designs of open channels.