Hydraulic Radius Calculator

If you want to find the hydraulic radius in your pipe flow calculations, then this hydraulic radius calculator is right up your alley. We gathered a total of five hydraulic radius equations for various channel shapes: a rectangle, a trapezoid, a triangle, and a pipe with a different level of fill — this tool is certainly not a pipe dream!

Come right in and discover what's the difference between a wetter diameter and the hydraulic radius of a pipe, or any other channel shape for that matter! Be sure also to check the pipe flow calculator, where we determine the flow velocity and discharge.

The hydraulic radius, R, is defined as the ratio of the cross sectional area of the flow, A, to the wetted perimeter of the channel, P:

R = A / P

For example, imagine that you have a rectangular channel, just like the one shown in the image. The area of the flow will be equal to the channel width, b, multiplied by the flow depth, y.

The wetted perimeter, on the other hand, is simply the total length of channel walls which are in contact with the liquid. In the case of the rectangular channel, it's a sum of b + y + y.

We have dedicated tools for calculating both mentioned measurements for various figures. Check the area calculator and perimeter calculator to see how they work!

The wetted perimeter of the pipe is the portion of the total pipe perimeter that is in contact with the flowing liquid (for example, water). It's very simple to calculate this for a full pipe — it's equal to the total pipe perimeter:

P = 2πr

If your pipe is only half full, the wetted perimeter will be equal to half of the total perimeter:

P = πr

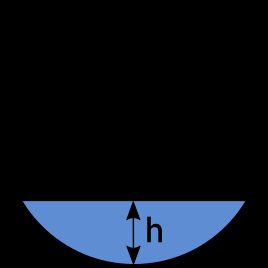
What happens if the pipe is not exactly full or half full? In that case, the wetted perimeter is equal to the arc length, corresponding to the central angle θ, as shown in the picture and in the equation below:

P = r × θ

where

θ = 2 × arccos [(r − h) / r]

This hydraulic radius calculator can be used for channels of various shapes, including rectangles, trapezoids, and triangles. Let's analyze them in more detail to find out which hydraulic radius equations can be used in each case.

1. Rectangular channel

In the case of a rectangular channel, the formulas are very straightforward. The hydraulic radius is simply equal to the rectangle's area divided by the wetted perimeter, as explained in the first example:

R = A / P = (b × y) / (b + y + y) = (b × y) / (b + 2y)

That's it — you can use this formula to find the hydraulic radius of a rectangular open channel.

2. Trapezoidal channel

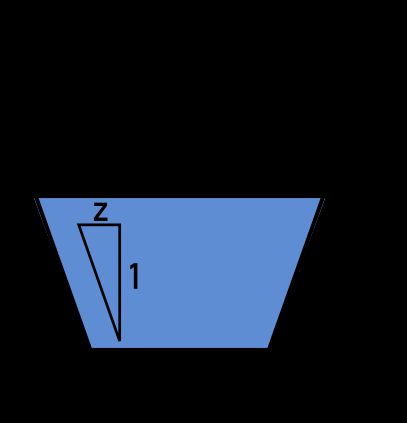
The formulas for the hydraulic radius of a trapezoidal channel are a bit more elaborate. First, let's recall the formula for the area of a trapezoid:

A = y × (B + b) / 2

We can simplify this formula when we use the value of slope, z, defined as the gain in width of the channel for every unit of its depth (the gradient of the trapezoid's non-parallel sides). Similar to the triangle rule, the gain in width on one side of the trapezoid is zy, and thus B = b + 2zy. Then:

A = by + y²z

The wetted perimeter is equal to b and the lengths of two sloped sides of the channel. Using the Pythagorean theorem, we find that:

P = b + 2 × y × √(1 + z²)

From here, we can conclude that:

R = A / P = (by + y²z) / [b + 2 × y × √(1 + z²)]

Tip: If you have trouble with trapezoids, then the trapezoid calculator might be the right place to start learning more about them.

3. Triangular channel

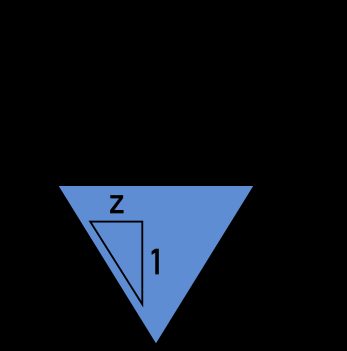
We can write down the area of a triangle in two ways — one way that uses the sides of the triangle and another that uses the slope, z:

A = B × y / 2 = y²z

The wetted perimeter of a triangle is analogous to that of a trapezoid, but this time, we sum only the sloped sides of the channel:

P = 2 × y × √(1 + z²)

Finally, we arrive at the hydraulic radius equation for a triangle:

R = A / P = y²z / [2 × y × √(1 + z²)] = yz / [2 × √(1 + z²)]

The other four options in our hydraulic radius calculator help you analyze pipes. Since the formulas differ, we identified two different cases: a pipe that's full and one that's less than full.

1. A full pipe

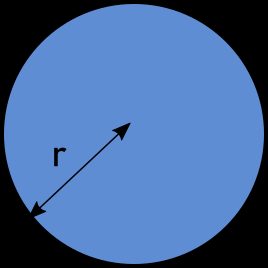
There's nothing easier than finding the hydraulic radius of a pipe completely filled with liquid. All you have to do is use the formulas for the area and perimeter of a circle!

R = A / P = πr² / 2πr = r/2

As you can see, the hydraulic radius of a full pipe is simply half of its radius.

2. Pipe (less than full)

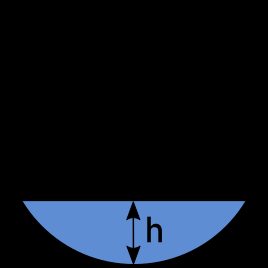
The problem gets a bit more complicated when the pipe is only partially filled. We already calculated this wetted perimeter in the wetted perimeter of a pipe section:

P = r × θ, where the central angle θ = 2 × arccos [(r − h) / r]

What about the area, then? You can use the segment area calculator or directly the formula for the circle segment area:

A = r² × (θ − sin(θ)) / 2

Combining the two, we find the hydraulic radius equation:

R = A / P = [r² × (θ − sin(θ)) / 2] / (r × θ)

This is quite a formula! Luckily, you can use this handy hydraulic radius calculator instead of meticulously performing all the calculations by hand ;)