Electric Potential Calculator

Use the electric potential calculator to determine the electric potential at a point either due to a single point charge or a system of point charges. You can also use this tool to find out the electrical potential difference between two points.

If you want to calculate the electric field due to a point charge, check out the electric field calculator.

Continue reading this article to learn:

• What is electric potential?
• What is the relation between electric potential and electric potential energy?
• How to calculate electric potential?
• What is the unit of electric potential?

To understand the idea of electric potential difference, let us consider some charge distribution. This charge distribution will produce an electric field. Now, if we want to move a small charge $q$ between any two points in this field, some work has to be done against the Coulomb force (you can use our Coulomb's law calculator to determine this force). This work done gets stored in the charge in the form of its electric potential energy.

If we consider two arbitrary points, say A and B, then the work done ($W_{AB}$) and the change in the potential energy ($\Delta U$) when the charge ($q$) moves from A to B can be written as:

• $W_{AB} = \Delta U = (V_A - V_B)q$ ...... (1)

where $V_A$ and $V_B$ are the electric potentials at A and B, respectively (we will explain what it means in the next section).

If the magnitude of $q$ is unity (we call a positive charge of unit magnitude as a test charge), the equation changes to:

• $\Delta V = (V_A - V_B) = \frac{W_{AB}}{q}$ ...... (2)

Using the above equation, we can define the electric potential difference ($\Delta V$) between the two points (B and A) as the work done to move a test charge from A to B against the electrostatic force.

Remember that the electric potential energy can't be calculated with the standard potential energy formula, $E=mgh$.

If we take one of the points in the previous section, say point A, at infinity and choose the potential at infinity to be zero, we can modify the electric potential difference formula (equation 2) as:

• $V_B = \frac{W_{\infty B}}{q}$

Hence, we can define the electric potential at any point as the amount of work done in moving a test charge from infinity to that point.

We can also define electric potential as the electric potential energy per unit charge, i.e.:

• $V = \frac{\Delta U}{q}$

So you can see that electric potential and electric potential energy are not the same things.

To calculate electric potential at any point A due to a single point charge (see figure 1), we will use the formula:

where:

• $q$ — Electrostatic charge;
• $r$ — Distance between A and the point charge; and
• $k = \frac{1}{4 \pi \epsilon_0}$ — Coulomb's constant.

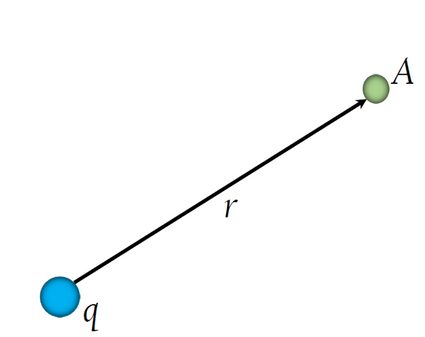
We note that when the charge $q$ is positive, the electric potential is positive. When the charge $q$ is negative electric potential is negative.

Now we will consider a case where there are four point charges, $q_1$, $q_2$, $q_3$, and $q_4$ (see figure 2). The potential at point A due to the charge $q_1$ is:

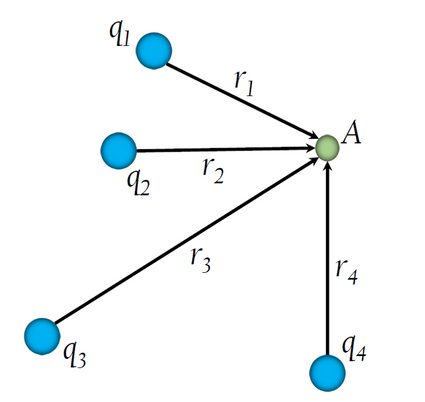
We can write similar expressions for the potential at A due to the other charges:

To get the resultant potential at A, we will use the superposition principle, i.e., we will add the individual potentials:

For a system of $n$ point charges, we can write the resultant potential as:

In the next section, we will see how to calculate electric potential using a simple example.

Let us calculate the electrostatic potential at a point due to a charge of $4 \times 10^{-7}\ \rm C$ located at a distance of $10\ \rm cm$.

1. We are given:

   $q = 4 \times 10^{-7}\ \rm C$ and $r = 10\ \rm cm$.

2. Substituting these values in the formula for electric potential due to a point charge, we get:

   $V = \frac{q}{4 \pi \epsilon_0 r}$

   $V = \frac{8.99 \times 10^9\ \rm N \cdot m^2/C^2 \times 4 \times 10^{-7}\ \rm C}{0.1\ m}$

   $V = 3.6 \times 10^4\ \rm V$

3. Hence, the electric potential at a point due to a charge of $4 \times 10^{-7}\ \rm C$ located at a distance of $10\ \rm cm$away is $3.6 \times 10^4\ \rm V$.

Now we will see how we can solve the same problem using our electric potential calculator:

1. Using the drop-down menu, choose electric potential due to a point charge.

2. Enter the value of electric charge, i.e., $4e-07$ and the distance between the point charge and the observation point ($10\ \rm cm$).

3. You can also change the value of relative permittivity using Advanced mode.

4. The calculator will display the value of the electric potential at the observation point, i.e., $3.595 \times 10^4 \ \rm V$.

The SI unit of electric potential is the volt (V). We can say that the electric potential at a point is 1 V if 1 J of work is done in carrying a positive charge of 1 C from infinity to that point against the electrostatic force.

The unit of potential difference is also the volt. You might be more familiar with voltage instead of the term potential difference. For example, when we talk about a 3 V battery, we simply mean that the potential difference between its two terminals is 3 V.

To write the dimensional formula for electric potential (or electric potential difference), we will first write the equation for electric potential:

• $V = \frac{W}{q}$

Now substituting the dimensional formula for work/energy and charge, we will get the dimensional formula for electric potential as:

To calculate the electric potential of a point charge (q) at a distance (r), follow the given instructions:

1. Multiply the charge q by Coulomb's constant.

2. Divide the value from step 1 by the distance r.

3. Congrats! You have calculated the electric potential of a point charge.

Yes, electric potential can be negative. The electrostatic potential at a point due to a positive charge is positive. If the charge is negative electric potential is also negative.

The electric potential difference between two points A and B is defined as the work done to move a positive unit charge from A to B. The SI unit of potential difference is volt (V).

Electric potential is a scalar quantity as it has no direction.

Electric potential is the electric potential energy per unit charge. The SI unit of electric potential energy is the joule (J), and that of charge is the coulomb (C). Hence, the SI unit of electric potential is J/C, i.e., the volt (V).

Zero. The electric potential at a point P due to a charge q is inversely proportional to the distance between them. Hence, when the distance is infinite, the electric potential is zero.