Displacement Calculator

In this displacement calculator, we will show you how to find displacement in a matter of seconds. We will also help you understand the displacement definition, and the displacement formula while we're at it.

What is displacement? What is the difference between displacements vs. distance? How to calculate displacement in physics? Find all the answers here!

Prefer watching over reading? Learn all you need in 90 seconds with this video we made for you:

Let's start from the beginning with the displacement definition. Displacement means different things in different contexts, so what is displacement in physics? In physics (and geometry), displacement is the amount an object has moved regardless of the path taken.

We will see this better when we look at the displacement formula, but displacement can be thought of as the distance between the starting point and the finishing point. It doesn't take into account the path taken to get from one point to the other, so it doesn't measure the distance traveled.

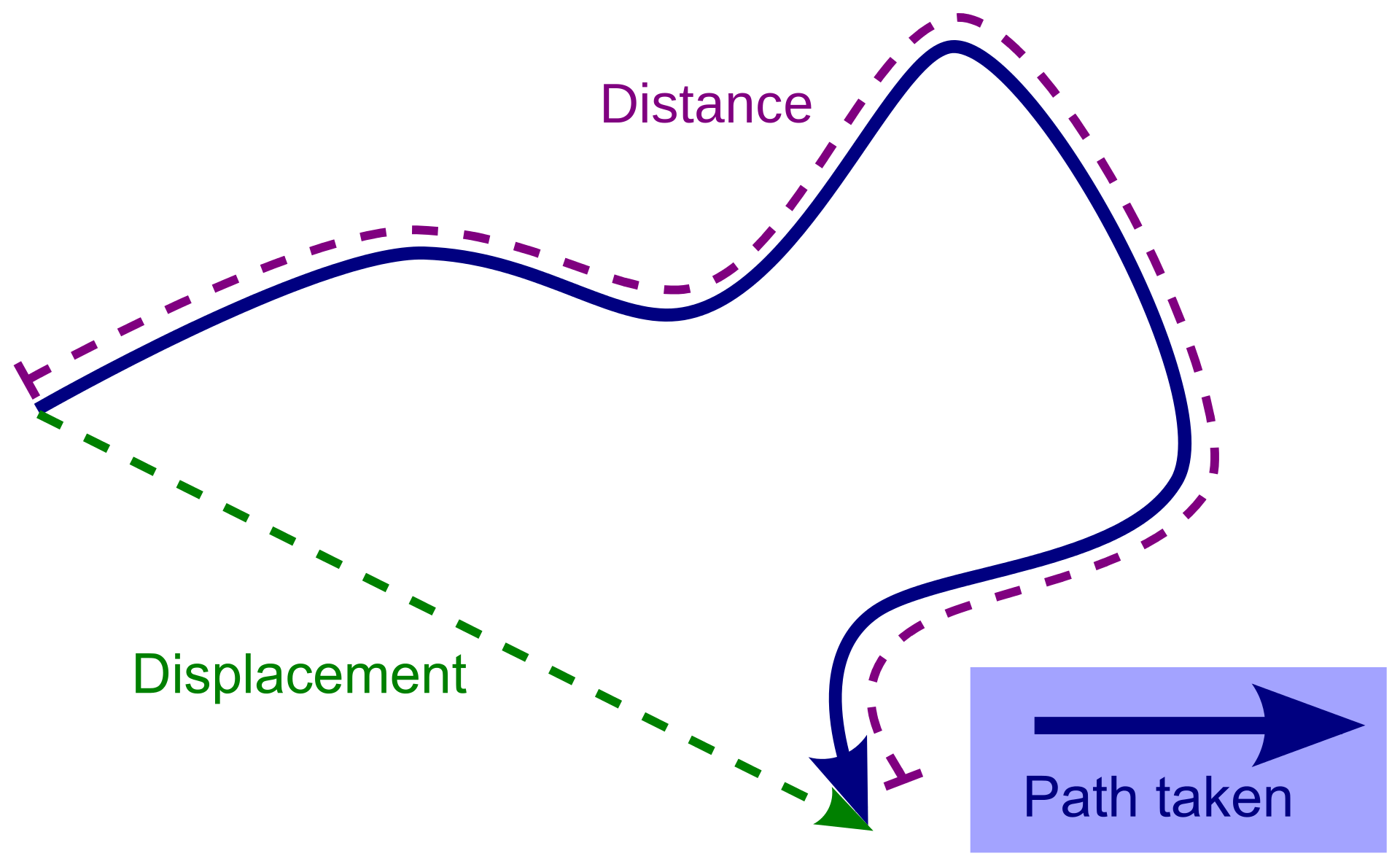
The distance between cities, for example, from New York to Washington, you have to travel depends on the route you take. However, no matter what road you choose, the final displacement will always be the same: the straight-line distance from one city to the other.

Did you know that another type of displacement is known as angular displacement! If you want to know more about it, check out our angular displacement calculator.

So, how to calculate displacement if it isn't the same as the distance traveled? The first thing to do is look at the displacement formula and forget about the displacement vs. distance debates. There are many formulations of the displacement formula, but the one we are interested in is this:

where,

• $d$ is the displacement;
• $t$ is the time taken from start to finish; and
• $v$ is the average velocity between the points.

Velocity is the crucial point here; we're not talking about speed. Velocity takes into account the direction of motion.

Since we are talking about displacement in physics, we can also calculate the average velocity using the acceleration calculator or the acceleration formula (if acceleration is constant):

where,

• $a$is the acceleration;
• $v_0$ is the initial velocity; and
• $v_1$ is the final velocity.

We can then find the displacement:

Alternatively, we could calculate the average velocity from a collection of velocities by doing a weighted average of them, where the weight of each velocity is the time spent at that velocity. You can do it conveniently using the weighted average calculator.

If you want to know how to find the average rate of change of distance with time (i.e., average velocity), check the average rate of change calculator.

In the displacement calculator that you see on your left, we have implemented three modes. The default, and most straightforward, way to find the displacement is by using a constant velocity. Increasing in complexity (and in number of inputs required), we next have a method that lets you calculate displacement by using the initial and final velocities, or the acceleration.

In the third mode of the displacement calculator, you can input up to 10 different velocities (and their respective times), and it will calculate the total displacement for you. As you fill one velocity in, a new one will appear.

Here is an example of how to find displacement from the acceleration and time:

1. Input the time the object is in movement.
2. Input the acceleration.
3. Input the initial or final velocity.
4. Watch as the resulting displacement is calculated for you.

As a bonus, we will also find the final/initial velocity for you.

Now that you've learned how to calculate the displacement, you might be wondering how it differs from the distance; we have you covered!

Displacement and distance are often confused, mostly because, in our daily lives, we always refer to both as distance. Displacement in physics (and geometry) is slightly different, in a very similar way as velocity differs from speed.

A logical way to think about the displacement vs. distance dilemma is that displacement is to velocity what distance is to speed. When you are using directionless speed, you get distance, so the length of the path traveled. On the other hand, using a vector-like velocity gets you the difference in position between the start and finish: the displacement.

Even though the distance is the most practical quantity in our normal lives, in physics, displacement takes center stage. Quantities like work depend on force and displacement, but not on distance.

The formula for displacement using velocity is:

d = v × t.

Here, d is the displacement, v is the average velocity from start to finish points, and t is the time taken to travel between those points. This formula assumes constant velocity.

To calculate displacement from acceleration:

1. Use the displacement formula for constant acceleration:

   d = (1/2) × at² + v₀t.

   Here d is the displacement, a is the acceleration, t is the time taken from start to finish, and the initial velocity is v₀.

2. Substitute the known values and solve for displacement.

No, displacement cannot be greater than distance. Displacement is the shortest distance between two points, a straight line. In contrast, distance represents the actual path length taken by an object from point A to point B, which may be longer than the displacement if the object follows an arbitrary path. However, the distance equals displacement if the object moves in a straight line from point A to point B.

The displacement is zero because the starting and final positions are the same, from home to work and back to home. Nevertheless, the distance covered in this 2 h commute at an average speed of 70 mph is 140 miles, calculated by using the formula:

d = v × t
d = 70 mph × 2 h = 140 mi