Delta to Wye Conversion

This delta to wye conversion calculator will help you transform a delta network of resistors to a wye network (or 'Y" network) and vice versa. In this calculator, you will learn:

• The difference between delta and wye networks of resistors;
• The formulas for delta to wye conversion;
• How to convert delta to wye networks;
• How to use our delta to wye conversion calculator; and
• Some applications of delta and wye networks of resistors.

Keep on reading to learn how to transform a complicated electronic circuit with wye and delta diagrams into a simple one (with only parallel and series-connected resistors) using the delta to "Y" conversion.

Our delta to wye conversion calculator is two calculators in one. Despite this, they are both relatively easy to use. To use this calculator, you first need to choose from the options wye to delta and delta to wye. Whatever you choose from these two options will make the calculator for that particular option available to you.

• So, if you choose the option delta to wye:

  1. Enter the resistance values R_a, R_b, and R_c for the delta network.

  2. The delta to wye converter will then return the resistance values R₁, R₂, and R₃ of the corresponding wye network.

• If, on the other hand, you choose the option wye to delta:

  1. Enter the resistance values for R₁, R₂, and R₃ of the wye network.

  2. The delta to wye converter will then return the resistance values R_a, R_b, and R_c of the corresponding in the delta network.

The default unit for measuring the resistances is ohm (Ω). But you can change it to other resistance measurement units from the given list of options. Remember to change the unit before you input the values.

Let's try out an example. For instance, you choose to convert wye to delta. You input the resistance values R₁, R₂, and R₃ as 5 Ω, 9 Ω, and 3 Ω, respectively. The calculator will instantly convert them to R_a, R_b, and R_c, resistances in the delta network as 17.4 Ω, 9.667 Ω, and 29 Ω, respectively.

Discover more about delta and wye networks by reading further.

In electronic circuits, the resistor (shown in the image below) is one of the most critical components and has a wide variety of uses. We can use resistors to limit the current in a circuit or the voltage flowing towards another component of the circuit.

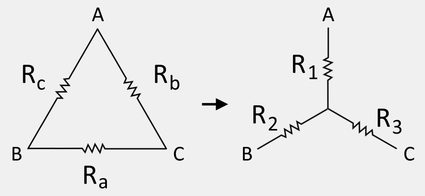
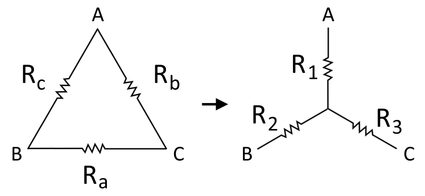
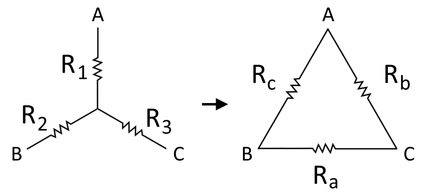
Since circuits can have multiple components, like capacitors, inductors, LEDs, motors, and so much more, circuits can also have many resistors in them. Resistors in circuits are usually connected in parallel or series but can sometimes form loops and multiple-branch networks, which we see in more complicated circuits. The simplest loop that resistors can make is the delta network, as shown in the diagram below:

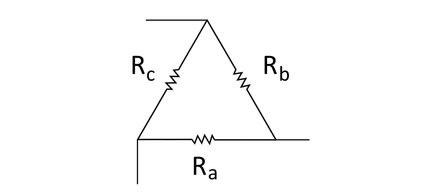
In electronic diagrams, we usually represent a resistor by a zigzag line. In a delta network, we connect three resistors to three nodes (represented by A, B, and C) that lead to three different parts of a circuit. We call it a "delta" network because, in its simplest diagrammatic representation, this network forms a triangular shape just like the uppercase Greek symbol delta Δ.

The difference between a delta and a wye network is that, in a wye network, we connect the said three nodes in a different fashion by extending the three nodes using three resistors and connecting all these resistors to a single node. This forms something like the letter Y, hence the name "wye" network. Here is what a wye network looks like:

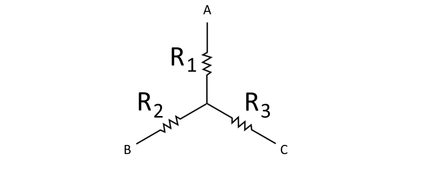
To perform a delta to wye conversion, we have to determine the set of resistors to use that will result in an equivalent overall network. The currents and voltages that pass through each of the three nodes must be the same in both types of networks. This is where our delta to wye conversion calculator comes in handy.

However, if you wish to learn how to convert delta to wye networks and vice versa, we will show you how to do so in the next section.

Knowing how to determine wye or delta networks in a circuit is the first step in conversion. Converting delta networks to wye networks is a matter of determining the "delta" in a circuit, knowing the resistance values of each resistor in the delta, and using the formulas we included in this text.

The same procedure also applies in the conversion of wye networks to delta networks. However, in this operation, we first have to determine which "wye" needs converting, then find the resistance values in each leg of the wye network. Finally, we substitute these values into the formulas provided below.

Delta to wye conversion formulas

where:

• R_a, R_b, R_c are the resistances in the delta network,
• R₁, R₂, R₃ are the resistances in the wye network.

Wye to delta conversion formulas

where, as previously seen:

• R_a, R_b, R_c are the resistances in the delta network,
• R₁, R₂, R₃ are the resistances in the wye network.

If you are looking at an actual circuit and you want to know the resistance value of a resistor without using a multimeter, you can tell it by looking at its color bands. You can use our resistor color code calculator to easily determine its corresponding resistance value. On the other hand, to further understand how to use the formulas above, let us consider an example in the next section of this text.

For our delta to y conversion (delta to wye conversion) calculation, let us consider the slightly complicated circuit shown below and convert the delta network (highlighted in green) to a wye network:

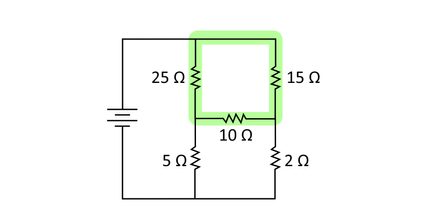
The delta diagram might seem different from the ones we showed earlier, but if you look closely, we can draw the delta shape like this:

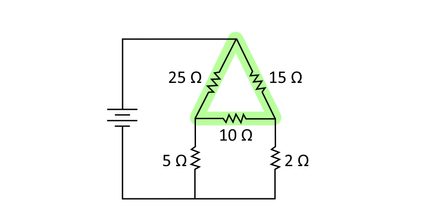
Now that we can see the familiar delta diagram in the circuit, let us now draw the corresponding equivalent wye network that our delta network will be transformed into. We can simply draw it over the delta network to preserve the location of the nodes, or we can draw the new wye network in a separate equivalent circuit. This is also the best time to label our resistors with the same variables we have in our formulas and reference diagram, as shown below:

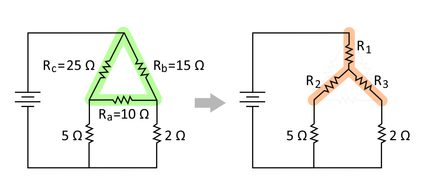
Once we have it all set up, we can now use the formulas we have for the delta to wye conversion to find the resistance values for each resistor in the equivalent wye network for the given circuit. Here is the calculation of each resistance value:

From these computations, we can now replace our delta network with a wye network using another set of resistors with resistance values of 7.5 Ω, 5.0 Ω, and 3.0 Ω for R₁, R₂, and R₃, respectively.

You may have noticed that in the example above, the original network did not have any parallel or series connections for any of the resistors. Instead, there were two deltas that cannot be simplified without the knowledge of delta to Y conversion.

After conversion, we can now see that R₂ resistor = 5 Ω is now in series with the other 5 Ω resistor. In that case, they can now be simplified even further by adding their resistance values together and replacing them with a single 10 Ω resistor. You can learn more about series resistors by checking out our series resistor calculator

With that said, delta to wye conversion, and vice versa, is the perfect method to simplify complicated circuitry when performing circuit analysis. We perform circuit analysis to determine the current or voltage flowing in our electronic circuit( three phase calculator), and it is best done with a simplified circuit or some parts of it.

If you find this calculator and text useful and informative, perhaps you would find our electricity cost calculator fun and valuable too. In there, you will learn how to calculate your electricity cost depending on the power you use at home.

Our engineers, Bogna and Ken, decided to make the lives of their fellow engineers easy by creating a resistance converter. A calculator that would simplify the process of converting resistances between delta and wye configurations. Thus helping electrical engineers in more efficient circuit analysis and design.

With a Master's in Civil Engineering, Bogna proves to be an invaluable asset, embodying the essence of a true catalyst in her field. From process management and organizing projects to creating tools for the betterment of others, she is a remarkable and credible individual in her field and beyond.

Kenneth Alambra exemplifies the essence of credibility via his Civil Engineering educational background, professional experience, and personal passions. He is a well-balanced mix of technical expertise, creative thinking, and continuous pursuit of knowledge, making him a distinctive and inspiring figure in his field.

We ensure our tools are based on authentic information and proper research. After an expert makes the calculator, another expert in the field reviews it thoroughly. Then, a native language speaker proofreads the content, ensuring further refinement; only then is the tool released for our users. To learn more about our commitment to quality, please refer to our Editorial Policies page.