Last updated: May 27, 2024

Angle of Repose Calculator

Created by Davide Borchia

Davide Borchia

Physicist by education, scientist by vocation. He holds a master’s degree in complex systems physics with a specialization in quantum technologies. If he is not reading something, he is outdoors trying to enjoy every bit of nature around him. He uses his memory as an advantage, and everything you will read from him contains at least one “I read about this five years ago” moment! See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

What is the angle of repose: definition and example How to calculate the angle of repose: formula and explanation An example: how to calculate the angle of repose of soil How to use our angle of repose calculator FAQs

Our angle of repose calculator can help you find a measure of the tendency of a granular material to flow or help you with your designs if you know the material's property and need to model its behavior.

Keep reading this short but exhaustive article to learn:

What is the angle of repose? Definition and scope of this quantity.
How to calculate the angle of repose formula: direct and inverse calculations.
And example of calculations of the repose angle: a soil pile.

And much more! What are you waiting for? Start pouring!

What is the angle of repose: definition and example

The angle of repose has a valid definition only for granular materials (think of sand, salt, flour...). In these cases, when a material is poured from above on a horizontal surface, it will eventually reach a point where its slope will not increase anymore. The angle formed with the horizontal plane is called angle of repose and is an intrinsic characteristic of the material and a few other parameters.

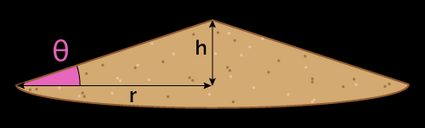
A pile of sand showing a small angle of repose — Sand has a relatively low angle of repose.

The angle of repose is a direct measure of the aptness of material to flow: the lower the angle, the more the material flows (think about it: water has an angle of repose of $0$ : it flows so well!), while for higher angles we witness materials that oppose to flowing. The granulometry of a material is one of the core elements that affect the angle of repose: the coarser the material, the higher the angle.

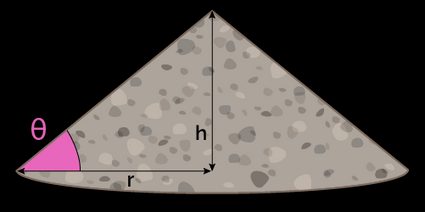
A heap of gravel shows a high angle of repose — Due to its coarseness, gravel has a higher angle of repose.

Once the pile of material reaches the associated angle of repose (all heaps start from angle $0\degree$ is built on a flat surface), the inclination of the slope won't increase anymore, and any additional material will flow down the side of the pile.

In the next section, we'll learn the formula to calculate the angle of repose: it's surprisingly easy!

How to calculate the angle of repose: formula and explanation

The calculations of the angle of repose rely heavily on the modelization of friction, in particular static friction, as we are interested in the behavior of the pile on the edge of flowing.

The formula for the angle of repose is:

\theta_\mathrm{r} = \arctan(\mu_\mathrm{s})

where:

$\theta_\mathrm{r}$ — Angle of repose;
$\mu_\mathrm{s}$ — Static friction coefficient; and
$\arctan$ — Inverse tangent function.

This formula quickly tells you what is the angle of repose for a given material. Notice how for lower static friction coefficients, the angle of repose is also low: this feature corresponds to materials that flow easily.

If you don't know the coefficient of static friction, or if the conditions are different than usual (for example, if the material is wet), you can use the relationship between the measurements of the pile to calculate the angle of repose:

\tan(\theta) = \frac{h}{r}=\frac{2\cdot h}{d}

where:

$r$ — Radius of the pile;
$d$ — Diameter of the pile ( $d=2\cdot r$ ); and
$h$ — Height of the pile.

To find this result, we used the property we met in the tangent calculator and the right triangle trigonometry calculator.

Notice that by considering the rules of trigonometry in right triangles and the formulas of the inclined plane calculator, we can find another expression for the friction coefficient in our setup:

\mu = \frac{m\cdot g\cdot \sin(\theta)}{m\cdot g \cdot \cos(\theta)}=\frac{\sin(\theta)}{\cos(\theta)}

where the coefficient is the ratio between the horizontal component of the force due to friction and the vertical component of the gravitational force (the normal force) acting on each grain of the material.

🙋 In the last formulas, we switched from $\mu_\mathrm{r}$ to $\mu$ , without index: this is because calculating the angle of repose of a pile starting by measurements on the heap itself calculates the coefficient of static friction for specific circumstances while starting from the tabulated values of $\mu_\mathrm{r}$ gives a forecasted value regardless of other factors.

An example: how to calculate the angle of repose of soil

Let's see how to calculate the angle of repose formula for soil. The friction coefficient for this material is variable, but we'll choose a reference value of $\mu_\mathrm{s} = 0.30$ . You know how to calculate the angle of repose of soil from this quantity:

\begin{split} \theta_\mathrm{r}& = \arctan(\mu_\mathrm{s}) = \arctan(0.3) \\ &= 16.7\degree \end{split}

Say you poured some soil on the ground, and a neat mound emerged. You measure the pile, and you find that:

$h = 0.35\ \mathrm{m}$ ; and
$d = 1.92\ \mathrm{m}$ .

Let's calculate the angle of repose in this situation:

\begin{split} \theta & = \arctan\left(\frac{h}{r}\right)\\[1em] &=\arctan\left(\frac{0.35\ \mathrm{m}}{0.96\ \mathrm{m}}\right)\\[1em] &=\arctan(0.3646) \approx 20\degree \end{split}

As you can see, the measured angle of repose is slightly higher than the forecasted one. Probably the soil is more humid or with coarser bits that oppose the flow.

🙋 Remember to mind the output of the inverse tangent function: in most calculators, it is in radians. In our tool, you can choose between degrees and radians, but to be sure about this conversion, we suggest you visit our angle conversion tool.

How to use our angle of repose calculator

Our angle of repose calculator implements both the formula to calculate the angle of repose starting from the friction coefficient and the one that uses the geometric measurements of the heap.

And this is not all the story! Our tool works in reverse: you can compute the friction coefficient or the forecasted size of the pile simply by inputting the angle of repose.

FAQs

What is the definition of angle of repose?

The angle of repose is formed by a pile of granular material with respect to a horizontal surface when it's poured from a height and allowed to flow freely. The angle represents the steepest slope where the material can lie without slipping down the side. Once the angle is reached, the pile grows, maintaining the ratio between height and radius constant.

How do I calculate the angle of repose?

To calculate the angle of repose, follow these simple steps:

Measure or find the coefficient of static friction of the desired material.
Calculate the inverse tangent of the coefficient.
Convert the result to the desired angle measurement unit.

That's it!

What is the angle of repose of sand?

Assuming that the coefficient of static friction of sand is 0.45, the angle of repose of sand is 24.23°. We can calculate the angle of repose of sand with the following simple steps:

Calculate the inverse tangent of the coefficient of friction:

arctan(0.45) = 0.42285 rad
Convert this quantity into degrees:

0.42285 rad × 180°/π = 24.23°

That's it: the pile will sit at a relatively shallow angle, as sand is a relatively well-flowing material.

How do I calculate the angle of repose from height and radius?

If you don't have access to the data relative to the friction coefficient of a material, you can calculate the angle of repose starting from the geometrical measurements of a pile. To do so, follow these simple steps:

Measure the height of the pile.
Measure the diameter of the pile, and divide by two to find the radius.
Calculate the ratio between height and radius.
Take the inverse tangent of the result.

That's it: the result is the angle of repose.