Music Interval Calculator
The music interval calculator helps you determine an interval between two notes. To find the interval between two pitches, choose from sounds in nine octaves and discover the simple and compound name for any distance greater than an octave. If you want to know an interval between notes, the calculator will differentiate between enharmonic equivalents (like C# and D♭, which denote the same sound) and give you also diminished and augmented intervals.
Intervals are one of the basic concepts of music theory. They are the building blocks of the different notes in a scale and chord construction, which in turn make up melodies and harmonies (you can learn the basics of harmonics at our harmonic series calculator). Understanding and recognizing them is essential for musicians as it makes it easier to play or sing by ear, write melodies, communicate with other musicians, and understand more complex ideas in music theory.
In the text below, you'll find a music intervals chart and a set of instructions on how to use the music interval calculator. You'll learn the smallest musical interval, how to find interval quality, and how to find the distance between two notes, like from F to C.
What is an interval in music?
A musical interval is the distance between two notes, which we can also describe as the difference in pitch between two sounds.
In physical terms, it is the ratio between the vibrational frequencies of notes.
Notes in music theory are sounds with determined frequencies. English-speaking countries named the sounds in the C major scale (the white keys on a piano) with the first seven letters of the Latin alphabet:
C, D, E, F, G, A, B
Another standard system for naming these sounds is solfège, which uses the syllables:
Do, Re, Mi, Fa, Sol, La, Si
Intervals may be counted in semitones. A semitone is the smallest unit of a musical distance commonly used in Western music. It is the distance between any two notes on adjacent keys (on a piano) or frets (on a guitar).
💡 Learn about how frets came to be with our fret calculator. 🎸
What is an octave?
Let's have a look at a piano keyboard:

On white keys, we have the sounds C, D, E, F, G, A, and B. You can see that after B, you have another C, then D, so the pattern repeats.
So, how do we differentiate between two Cs if we need to? We use the scientific notation — we add a number next to the letter, so we have C1, C2, C3, etc.
The interval (distance) between two notes, e.g., between C1 and C2 or F3 and F4, is called an octave. When we go an octave up, we double the frequency. For example:
A4 = 440 HzA5 = 880 HzA6 = 1760 Hz
While the number of semitones between two notes is the same in any octave, i.e., there's one semitone between E4 to F4, and E8 to F8, the frequency distance in hertz between these two is not the same. To determine the distance in semitones and in hertz between two given notes, you can use the semitone calculator.
Accidentals in music
We've covered the white keys, but what about the black ones?
We use the sharp ♯ and flat ♭ symbols, along with the letters, to designate the sounds on the black keys. The sharp raises the note by a semitone (the smallest musical interval), while the flat lowers it by one.
The black key between C and D can be called C# or D♭. Notes with these two names have the same pitch, but which name you should use depends on the musical context.
If we play each note on a piano one by one from left to right, we get 12 tones which make up the chromatic scale:
C C#/D♭ D D#/E♭ E F F#/G♭ G G#/A♭ A A#/B♭ B
In this scale, the distance between any two adjacent notes is one semitone. E and F and B and C are the two pairs of white keys which don't have a black key between them, as they are a semitone apart anyway.
Musical intervals chart
Ok, this is the exciting moment where you learn the names of the intervals!
The smallest musical interval (not counting a unison/prime, where the notes are the same, e.g., between C1 and C1) is the minor second. It's equal to one semitone, so a minor second is, for example, the interval between G and A♭.
If you go from C to D, you will go up by a tone (two semitones), which is known as a major second. Below you can see the names of the intervals up to and including an octave and the corresponding number of semitones.
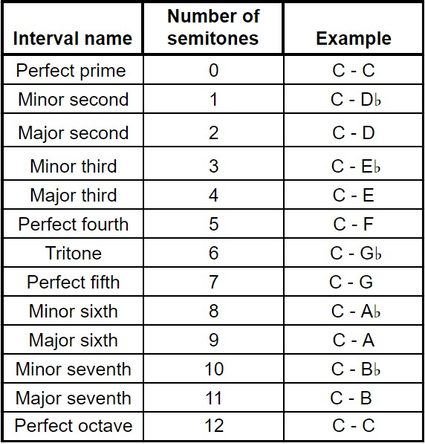
💡 A tritone is also called an augmented fourth or a diminished fifth (depending on the context).
How to use the music interval calculator
We divided the music interval calculator into two parts. The first one deals with intervals between pitches, and the second — notes as units of music theory.
What is the difference?
You should use the first one when you want to know an interval between two sounds. For example, between a piano key, which we denote by C, and another one denoted by C♯ or D♭. The interval between the sounds produced by these two keys is a minor second. We don’t use the augmented and diminished intervals here, as you would never talk about an augmented prime if somebody sang two sounds to you and asked what interval it is.
BUT the interval between C and C♯ IS NOT a minor second (but the one between C and D♭ is). When you want to find the interval between notes from their letters or symbols on a staff, you should use the “between notes” part of the calculator. It will tell you the interval between C and C# is an augmented prime. Notes often appear in a musical context, like a scale or key, when diminishing and augmenting matters.
If you want to find an interval between two notes (e.g., on a music theory test 😉), leave the interval type in the calculator as the default and simply choose the names of the notes. Remember, note 1 has to be lower than note 2. Check the Show semitones/tones option if you want to see the corresponding number of tones and semitones.
If you want to know an interval between two sounds:
- Change the "interval type" in the first field.
- Choose the note and octave by which we denote the first sound.
- Choose the note and octave by which we denote the second sound.
- At the bottom of the music interval calculator, you'll see the interval between the two pitches. If you want to know the number of semitones and tones that make up the interval — choose the
Show semitones/tonesoption.
Note:
-
Intervals larger than an octave are called "compound intervals". They can be thought of as a certain number of octaves + the remaining interval.
-
For intervals that have between 13 and 28 semitones, you'll see both the simple and the compound names.
-
Intervals with more than 28 semitones (major seventeenth) will only have a compound name, as they are very rarely known by anything else. So, for example, you'll see "two octaves plus a fifth" instead of a 19th.
Determine an interval between two pitches
Learn the number of semitones in all of the simple intervals. Then count how many keys on a piano (or frets on a guitar) you must go from note 1 to note 2.
Example: you want to know the interval between sounds corresponding to keys C and E.
First, count the distance between keys — there are 4 semitones. Then you look at the musical intervals chart and see that 4 semitones correspond to a major third.
Alternatively, you can go from note 1 to note 2, naming all the intervals instead of counting semitones.
Determine an interval between two notes
Intervals consist of a number (second, third, fourth) and their quality (minor, major, perfect). To check the interval between two notes:
-
Identify the number — erase the accidentals (
C#becomesC,B♭becomesB, etc.), then count the steps as if we were using a C-major scale. For example, fromG#toE, you count:G (1), A (2), B (3), C (4), D (5), E (6)E is the sixth note, so the interval is a sixth.
-
Identify the interval quality by counting the semitones between the notes, still ignoring the accidentals.
For example, we have 9 semitones between
GandE(check with a keyboard), which makes it a major sixth. -
Adjust for accidentals:
- If the notes have no accidentals or they are the same in both notes (
F#andG#,B♭andA♭, etc.), the interval from step 2 stays the same.
Otherwise:
- "
♭" next to the lower note increases the interval, "♯" decreases it; - "
♭" next to the higher note decreases the interval, "♯" increases it.
Now, if you decrease an interval by a semitone:
- If it's major, it changes to minor;
- If it's minor or perfect, it changes to diminished; and
- If it's diminished, it changes to doubly diminished.
If you increase an interval by a semitone:
-
If it's minor, it changes to major;
-
If it's major or perfect, it changes to augmented; and
-
If it's augmented, it changes to doubly augmented.
Let's find an interval between
A#andC:- Count the steps for the notes without accidentals:
A (1), B(2); C (3)— it's a third.
2. BetweenAandC, there are 3 semitones — it's a minor third.
3. We have to decrease the interval because of the sharp sign. The minor third becomes a diminished third. - If the notes have no accidentals or they are the same in both notes (
How to get from F to C — examples
-
From
FtoCwe count:F (1), G (2), A (3), B (4), C (5)We finished at 5, so the interval is a fifth. There are 7 semitones (check on a keyboard), so it's a perfect fifth. No accidentals here, so it stays perfect.
-
From
CtoFwe count:C (1), D (2), E (3), F (4)Fourth. 5 semitones — it's a perfect fourth.
-
CtoF#:At first, we ignore the accidental:
C (1), D (2), E (3), F (4)We know the number — a fourth. But we have to go one semitone higher to reach
F#. We have to augment the perfect fourth, so the interval will be the augmented fourth. -
CtoA:C (1), D (2), E (3), F (4), G (5), A (6)It's a sixth. 9 semitones make it a major sixth.
-
CtoA♭:At first, we ignore the accidental and count:
C (1), D (2), E (3), F (4), G (5), A (6)It's a sixth. Between
CandAthere are 9 semitones, so it's a major sixth. There's a flat sign next to the higher note, so we have to decrease the interval by a semitone. Therefore, it will be a minor sixth. -
Now something tricky:
F#toB♭:
-
We count the steps for the notes without accidentals:
F (1), G (2), A (3), B (4)It's a fourth.
-
6 semitones between
FandBindicate it's a tritone. Tritone, depending on the context, is called an augmented fourth or a diminished fifth. We know from step 1 that it needs to be a fourth, so we have an augmented fourth. -
#next to the lower note means we have to decrease the semitone. It becomes a perfect fourth.♭next to the higher low means we have to decrease it one more time. Perfect changes to diminished, so we end up with the diminished fourth.
You can practice this way with any notes, and check with the music interval calculator if you got the interval right.
FAQs
Why was the tritone an unacceptable interval in music?
The tritone (also known as the augmented fourth and the diminished fifth). In isolation, it sounds dissonant, and this dissonance made people associate it with the devil. However, the tritone appears in many chords like the dominant seventh, but then it's disguised among other notes and intervals.
How do I determine the interval between two notes?
Here's how you can determine two notes' interval:
- Remove the notes' accidentals and count the C-major scale's steps between them (e.g.
EtoB♭becomesEtoBand is five notes). - Identify the interval (e.g. a perfect fifth).
- Adjust for the accidentals (e.g. the
B♭has a flat, so the interval becomes a diminished fifth). - Voila! You have the interval between two notes!
What is the smallest interval in tonal music?
The smallest distance between two notes in tonal music is the semitone, which corresponds to the minor second interval. Tonal music is the music we're all used to, and is the music system where intervals are most well-defined.