Fret Calculator
This fret calculator will help you determine the proper spacing your DIY guitar frets need to have for it to sound like an actual guitar does. This calculator is perfect if you plan to build your very own guitar from scratch. You can also use this calculator for any stringed instrument that follows the Western Chromatic Scale. To learn more about the fret placement formula and the mathematics behind it, read on!
What are frets?

Stringed musical instruments, like the guitar, ukulele, or banjo, share the same fundamental structure. One of the parts that they have in common is frets. Frets can be seen on the fingerboard and are crucial in producing beautiful music. Luthiers (builders of string instruments) commonly use metal for the frets, and they need to be placed along the fingerboard with a particular spacing pattern for the instrument to sound right.
The wave equations, and the assumptions made by the famous mathematician and philosopher Pythagoras, define the origin of the spacing formula. The spacing formula breaks down the original scale length (which is the total length of an open string from nut to bridge) to determine the new scale length from the first fret to the bridge, and so on and so forth. To better understand this, let us derive this formula using the concepts we know.
Concepts we need
The fret placement formula is a combination of three equations, two of which are physics formulas, and the other is an assumption that we now consider standard. Without further ado, here are the concepts:
"Pythagorean Equation"
Pythagoras, the same person who discovered the Pythagorean theorem of a² + b² = c², found that for a string instrument to sound its "best", any two adjacent notes played on the same string should have the same standard ratio. Since we can distinguish sounds through their frequencies, a change in the pitch of a sound also means a change in its frequency - the higher the frequency of a sound is, the higher its pitch is.
Adjusting a sound's pitch to predetermined frequencies is how we produce notes. In a string instrument, pressing on the string at the first fret shortens the scale length of the string. Plucking the new shortened scale length produces a higher frequency compared to just plucking an open string. And since, according to Pythagoras, any two adjacent notes should have the same common ratio, we can express this in a series of equations:
f₁ / f₀ = c
f₂ / f₁ = c
f₃ / f₂ = c
And so on and so forth. Where "c" is the said standard ratio, f₀ is the frequency of the open string, and f₁, f₂, and f₃ are the frequencies of the following notes while pressing on the 1st, 2nd, and 3rd frets, respectively.
Rearranging these equations and following this trend, we can come up with a set of equations as follows:
Equation 1: f₁ = c × f₀
Equation 2: f₂ = c × f₁
Equation 3: f₃ = c × f₂
Substituting f₁ in Equation 2 with the equivalent expression in Equation 1, we obtain:
f₂ = c × (c × f₀)
f₂ = c² × f₀ (Equation 4)
The same goes when we substitute Equation 4 in Equation 3. We can express f₃ in terms of f₀ as follows:
f₃ = c × (c² × f₀)
f₃ = c³ × f₀
Continuing this fashion, we can generalize this equation by:
fn = cⁿ × f₀; where fn is the frequency of a note produced while pressing at the "nth" fret.
Let's call this equation the "Pythagorean equation." This is our first equation.
Chromatic scale
Our second equation comes from the world of music, which states that a frequency and double that frequency produce two similar sounds, but at exactly one "octave" higher. An octave is a set of 12 tones determined by a scale convention we call the chromatic scale. In this convention, we designate the notes in the scale as follows:
C, C#, D, D#, E, F, F#, G, G#, A, A#, and B.
Each interval represents a half step up, following the increase of frequency at a rate "c," as described above. D#, read as "d-sharp," is half a step up D. It also means that the frequency of D# is equal to the frequency of D multiplied by "c." Theoretically speaking, we can consider a jump from C to D as one whole step with an increase in the frequency of c². To learn more about music note intervals, you can check our music interval calculator.
In the Western chromatic scale, it has been the standard to use such notations to represent each note in the scale. We can repeat these 12 notes also to represent the notes on the next octave. However, to make them distinct from each other, we can use numbers to do this. For example, we can continue the above succession into the next octave:
C, C#, D, D#, E, F, F#, G, G#, A, A#, B, C1, C1#, D1, D1#, E1, F1, F1#, G1, G1#, and so forth...
Extending the observation that we can produce two similar sounds after 12 notes, but with a doubled frequency, we can say that:
f₁₂ = 2 × f₀
Going back to Pythagoras' equation, we can say that f₁₂ is also equal to f₀ times c¹² as expressed in this equation:
f₁₂ = 2 × f₀ = (c¹²) × f₀
With this relationship, we can cancel out f₀ from both sides of the equation, leaving us with an equation that we can use to solve for the value of our constant c:
2 × f₀ = (c¹²) × f₀
2 = c¹²
21/12 = (c¹²)1/12
21/12 = c
c = 1.0594630943593 ≈ 1.059463
Frequency equation
Now that we have the value of c, we are close to finally achieving the fret placement formula. With this, we would need the help of a physics theory that relates the frequency and the length of a vibrating string. In physics, we know that the frequency of a wave is indirectly proportional to its wavelength. Considering a non-elastic string fixed on both ends, the relationship between the frequency and its wavelength is as follows:
f = v / (2 × L) → fn = v / (2 × Ln)
where v is the velocity of the string of constant tension and diameter, and Lₙ is the length of the string from any fret "n" to the bridge. You can learn more about wavelengths by visiting our wavelength calculator and our simple harmonic motion calculator.
Deriving the fret placement formula
With these equations ready, we can now consider n=0, so we can have f₀ = v / (2 × L₀), where L₀ is simply our initial scale length. We can then combine this equation with fn = (cⁿ) × f₀ and fn = v / (2 × Ln) to obtain the relationship of Ln and L₀ in terms of "c", as shown in the steps below:
-
Substituting f₀ = v / (2 × L₀) to fn = (cⁿ) × f₀", we get: fn = (cⁿ) × (v / 2 × L₀)
-
Equating fn = (cⁿ) × (v / 2 × L₀) to fn = v / (2 × Ln), we now have: (cⁿ) × (v / 2 × L₀) = v / (2 × Ln)
-
Simplifying, we can cancel out (v / 2) on both sides, leaving us with: (cⁿ) / L₀ = 1 / Ln
-
Reciprocating this equation, we now have the formula for the distance of any fret from the bridge: Ln = L₀ / (cⁿ).
We can already stop here. However, measuring your ukulele or guitar fret placement from the nut of the instrument would be so much better than measuring it from the bridge. With that said, we can then subtract the Ln values from L₀ to give us the distances of the frets from the nut, as shown in the following formula:
distance from the nut = L₀ - (L₀ / (cⁿ))
= L₀ - (L₀ × 1 / (cⁿ))
= L₀ - (L₀ × (1 / c)ⁿ)
= L₀ - (L₀ × (1 / 1.059463)ⁿ)
= L₀ - (L₀ × (0.943874312681693)ⁿ)
= L₀ - (L₀ × (0.9438743)ⁿ)
= L₀ × (1 - (0.9438743ⁿ))
Here is an illustration to help you visualize the scale lengths and distances described above:
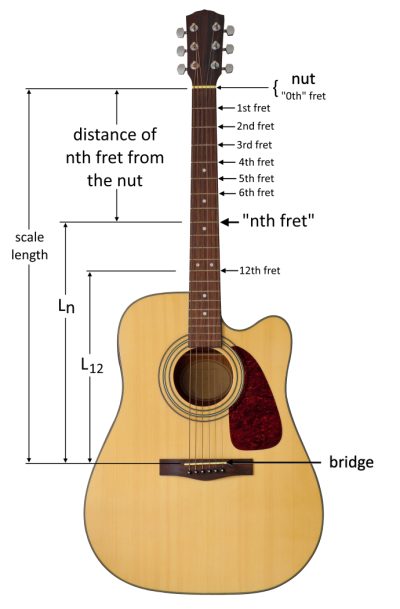
How to use this fret calculator
In building your own DIY guitar or any western string instrument, you must first determine your preferred scale length. Standard guitars have around 25 to 26 inches (63 to 65 cm) of scale length. Just type that into our fret calculator and it will instantly show the distances, from the nut, of each of your frets.