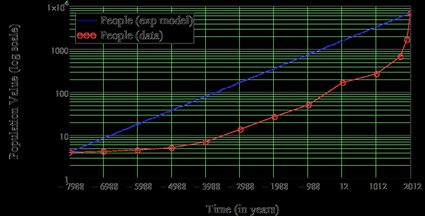
Welcome to the vampire apocalypse calculator, you lovely, tasty human. This sophisticated tool is based on the predator - prey model, a model which successfully describes the dynamics of ecosystems, chemical reactions, and even economics. Now it's time to use it to answer the question: what if vampires were among us? You might think we're joking, but the facts are clear. If we compare the actual (red points) to the exponential growth model (blue line), it reveals there are some hidden causes preventing the expansion of humanity.
We could theorize all day why this is, but there's one idea we'd like to check and discuss: vampires. Are you ready to unveil the ancient mysteries of vampirism?
What is vampirism?
Nearly every culture around the world has its blood-drinking creature. The ancient world had the female demons Lilith (Babylonia) and Lamia (Greece). In Africa, the Ewe folklore believes in Adze - a vampiric being that can take the form of a firefly. Chilean Peuchen was a gigantic flying snake that could paralyse, and, in Asia, Penanggal was a woman who broke a pact with the devil and has been forever cursed to become a bloodsucking demon. So, why is it that vampires are known around the globe? Isn't it suspicious?
What about the vampires themselves? They are usually believed to be undead creatures with supernatural powers; they don't age, can fly, and can fully regenerate from almost any wound. They have a taste for human blood, but are afraid of sunlight, silver, religious symbols, and garlic. Vampires can be killed by decapitation or a wooden stake through the heart. The last important thing is that vampires can't reproduce - they can only turn a human into a vampire.

How to use the vampire apocalypse calculator?
What if vampires were among us? The vampire apocalypse calculator allows you to check how humanity would fair in some selected scenarios from popular books and movies, as well as creating your own story from scratch. It's your decision! We present the result in the form of a graph that plots how three populations change: humans (blue points), vampires (red points), and vampire slayers (yellow points). Adjust the graph if needed by setting an appropriate time scale (days, weeks, months, years, decades, centuries) and type of chart (linear or logarithmic).
The vampire apocalypse calculator performs real-time numerical calculations that might sometimes be a little demanding, depending on your machine specifications. But, please, be understanding! The algorithm can receive up to 13 parameters from the three species:
-
Humans - if not interrupted by vampires, their population size will grow exponentially. The available settings are the initial population, the probability of turning into a vampire when attacked, and annual population growth. Humans' unique ability is to grow faster when their population becomes smaller than its starting value.
-
Vampires - bloodthirsty humanoids that hunt people and turn them into new vampires. The available parameters are their initial population and their aggression level towards humans and slayers. You can make vampires smarter with their special ability. When activated, vampires will refrain from killing too many humans, so they do not lose their only source of blood.
-
Vampire slayers - an organization of brave people with one objective: save the world from vampiric domination. The available parameters are their initial population, annual recruitment speed, aggression level towards vampires, and vampire transformation probability. They cannot afford their member's salaries if the entire world is a vampire hunter, so you can turn on the vampire slayers special ability to limit the maximum size of the organization.
Go ahead and test our vampire apocalypse calculator! If you find a set of parameters that creates an incredible story, don't hesitate and share it with your friends and us. You can use the Send this result button just below the graph.
For example, let's build a custom scenario (Select a scenario: Custom). A city with one million people (Humans - Initial population: 1,000,000) that is growing every year at typical speed (Humans - Annual population growth: current (1% per year)). Suddenly, 200 of vampires (Vampires - Initial population: 200) invaded it and started attacking people from time to time (Vampires - vs. humans: common attacks) having the human-vampire transformation probability of one half (Humans - Transformation probability: 50%). What can you see on the resulting graph? Actually, not much; the time scale is too low. After increasing it (Time scale: decades), the picture is entirely different! You can see that mankind will be wiped out after about 48 decades. Now, how many vampire slayers would you need to save humanity? Try playing with different options!
🙋 Why not create your own Minecraft vampire world? Take a look at the Minecraft circle generator or the Nether portal calculator to help you with some of the details! 🦇
Predator - prey Model: Lotka - Volterra equations
Italian astronomer and physicist Galileo Galilei (known for his experiments with falling bodies and inclined planes) once said Mathematics is the language in which God has written the universe. Indeed, scientists all around the world try to find suitable mathematical equations that describe the natural world properly.
If you consider a simple ecosystem with two species, e.g., foxes and rabbits, the Lotka - Volterra equations generally work just fine. They are also called the predator - prey model. Why? Let's stick with our example. The population of rabbits can peacefully live and reproduce if we assume that they have access to an unlimited source of food in the forest. On the other hand, foxes are carnivorous, so their population size depends on the accessibility of food, i.e., rabbits. Can you see where the problem is? More rabbits mean more foxes, but more foxes mean fewer rabbits.
A similar situation exists with humans (prey) and vampires (predators). Our calculator makes use of the Lotka - Volterra equations, with a few modifications. First of all, we created some vampire slayers that control the population of vampires. Secondly, we gave each group a special ability that is implemented indirectly in the algorithm. Eventually, we came up with the following differential equations:
where:
- , , and are the sizes of the human, vampire, and vampire slayers populations respectively.
- and are the growth rates of the human and vampire slayer populations.
- and are the probabilities that a human and a vampire slayer will turn into a vampire.
- Coefficients , , and describe the aggression levels: vampire towards a human, vampire towards vampire slayer, and vampire slayer towards vampire respectively.
For more explanations, read the , an article published in Applied Mathematical Sciences. We based this calculator on the fourth-order Runge-Kutta method to solve the problem of differential equations.
Bloodsuckers - are vampires among us?
There are species in the animal kingdom that suck and feed on prey's blood. We call this practice hematophagy, and many small animals prefer it since blood is basically a fluid tissue rich in nutrients. What's the main difference between animal bloodsuckers and fictitious vampires? The former can't turn a victim into another creature by biting or killing it. Lucky for us! Some known bloodsucking animals are:
-
Vampire Bats - they mainly hunt birds and reptiles, but they occasionally turn their fangs on humans. Interestingly, vampire bats often share the blood that they have sucked with their hungry compatriots. That's a real friendship!
-
Leechs - bloodsucking worms that live in water. They can be used medicinally, as they can restore blood flow to damaged veins.
-
Vampire Finches - don't let these lovely looking birds deceive you! When other food sources are scarce, they sometimes feed by drinking the blood of other bigger birds.
-
Mosquitoes - flying insects that you're probably familiar with. They can be dangerous to humans since mosquitoes can carry many diseases. An interesting fact is that only female mosquitoes suck blood from their victims (they need it to fuel egg production).

Humans also practice hematophagy! There are meals that contain animal blood. For example, some societies around the world eat blood sausages - sausages filled with blood that has been cooked or dried. With that, we can conclude that vampires are actually among us! (of course, it's only a half-truth; real bloodsuckers can't turn people into vampires).
🙋 How would you grade this calculator? with an A? or an A+? 😅 With the test grade calculator you can find out the equivalence of grades in letters and percentages.