Hamming Distance Calculator

With our Hamming distance calculator, you will learn why the distance from $01$ to $10$ is $2$ and not $9$ — at least sometimes!

Are you ready for a short dive into information theory? Here you will learn:

• What is the Hamming distance?
• How to calculate the Hamming distance?
• Where do we apply the Hamming distance?

The Hamming distance is a metric used in information theory to measure how much two messages with the same length differ.

For message, we mean a string: whenever you see a number in this article, you should remember that the digits are no more than letters of an alphabet, and you can't perform mathematical operations on them!

The Hamming distance indicates the number of different digits/letters in a pair of messages. Take the words "Hamming" and "humming": what is the Hamming distance?

Let's see. "Hamming" and "humming" — there is one letter of difference, so the Hamming distance is 1.

Increase the Hamming distance to two: farming, humping, camping. As you can see, there are a few examples. If we increase the Hamming distance to three, there is even more: fasting, hosting, hammock or Hamburg.

As you can see, the higher the Hamming distance, the more difficult it is to "see" the original word: that's because we accumulated errors.

The Hamming distance is a fundamental concept in the field of error detection and correction. An error in a message is quantifiable by measuring the number of different bits between the corrupted message and the original one.

The Hamming distance in an error-correcting code defines the capacity of an algorithm to detect and correct an error. The higher the distance, the higher the number of possible messages between two valid codewords, allowing more space to identify the error. You can learn more on this complex topic with our Hamming codes calculator!

In computer science, the Hamming distance is usually relegated to strings of numbers: letters lie at a higher level!

We will give you a hint on how to calculate the Hamming distance in a binary and a decimal message.

Take two binary messages with equal length, and write them down:

Now compare the messages "bitwise", and mark on one of them where the values of the bit in a given position differ between the messages:

Then count the number of bits you found: that is the Hamming distance. For short messages, it doesn't take long to calculate, but on longer ones, it can take a while — that's why we made this calculator!

You can apply the same procedure for any other message, in any alphabet. In our Hamming distance calculator, we implemented the decimal system too. Let's see an example of Hamming distance with ten digits!

Mark and count where different digits lie in the same position:

The Hamming distance in this case is $3$. Easy, isn't it?

There is a neat way to visualize the Hamming distance — it uses geometry to represent the various codewords and find a path connecting them.

This representation can get messy pretty quickly, so don't rely on it to calculate the Hamming distance: writing down the string is usually enough!

Let's start with the simplest of the messages: one binary bit. Our bit can assume a value of either $0$ or $1$.

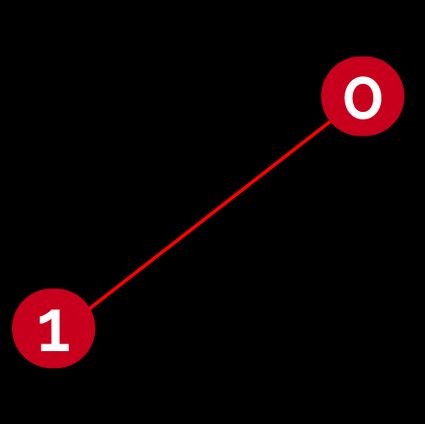
Assuming the presence of a corruption, we can visualize the path (in red) that connects the two states. In this case, the path is made of a single segment: the Hamming distance is $1$.

We now increase the number of bits to two: how many messages can we build? The answer is four, and we can represent them on a square!

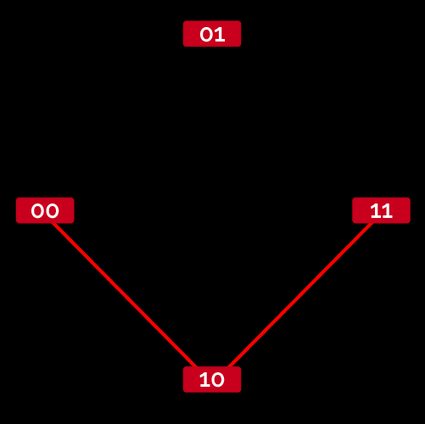
Let's corrupt two bits: from $00$ we pass to $11$. To connect them, we need to depart from $00$, visit either $01$ or $10$, and arrive at $11$, thus traveling two line segments: the Hamming distance is $2$.

We can do it again! Add another bit; which shape will you get?

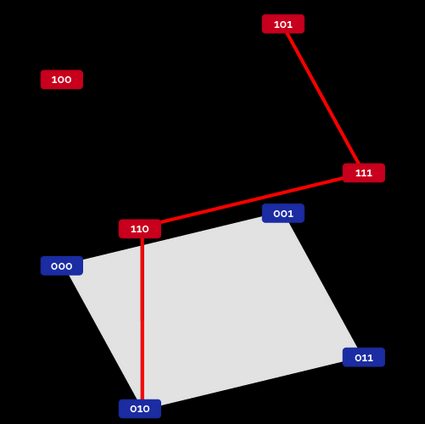
A cube, exactly! We created two "levels": in each one, the last two bits are the same as the previous example: the Hamming distance can be at most $2$ if you stay on one "floor". Adding another "floor" allows us to increase the maximum distance to $3$.

Follow the example highlighted in red above:

We visited two intermediate states and walked three segments. Notice how multiple minimal paths connect the two selected states: in this case, there are $6$ of them. Can you find them all?

Let's increase the number of bits one last time: now our message is four bits long, and the corresponding shape is a hypercube, a four-dimensional shape that we can represent in our 3D space with two "concentric" cubes. Take a look!

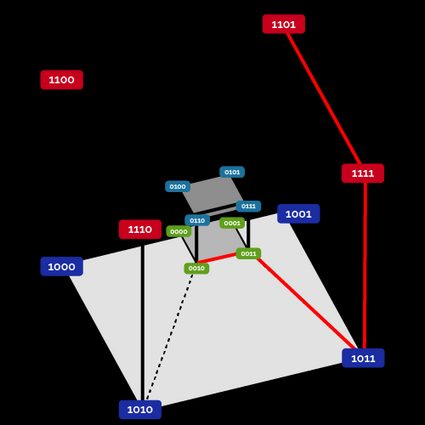
Now we can reach a Hamming distance as big as $4$. We chose a single path to show that, but obviously, the number of possible paths is high!

Let's sum the representations:

• $1$ bits: a segment, the maximum Hamming distance is $1$;
• $2$ bits: a square, the maximum Hamming distance is $2$;
• $3$ bits: a cube, the maximum Hamming distance is $3$;
• $4$ bits: a hypercube, the maximum Hamming distance is $4$.

Isn't it obvious? You can flip only as many bits as the length of the message to create any other codeword!

There is nothing easier than using our Hamming distance calculator! Choose the numerical system you desire, and input the two messages: we will give you the Hamming distance in the blink of an eye!

The Hamming distance between 10101 and 01100 is 3. The two messages differ in positions number 1, 2, and 5. A Hamming distance of 3 on a message with length 5 means that more than half of the digits changed: it is hard to see the original message, as the corruption is pretty high!

To calculate the Hamming distance, you simply count the number of bits where two same-length messages differ. An example of Hamming distance 1 is the distance between 1101 and 1001. If you increase the distance to 2, we can give as an example 1001 and 1010.

The Hamming distance is a metric (in the mathematical sense) used in error correction theory to measure the distance between two codewords. In detail, the Hamming distance measures the number of different bits in two strings of the same length.

In computer science, distance metrics are a way to measure similarity between data. They don't measure a physical distance between two points in space but the distance of two "codewords" in their relative abstract spaces.

Distance metrics are of great importance in error detection and correction and in machine learning.