GSD Calculator – Ground Sample Distance
The GSD calculator will determine the ground sample distance for photogrammetry and aerial surveying purposes. Modern drone technology enables mapping croplands for longer periods of time (see drone flight time calculator).
Aerial surveying is a method of collecting geomatic data using aircraft, drones, or balloons. The concept of ground sample distance is useful in obtaining useful data from the imagery. You can either use GSD to take measurements or to determine the surveying requirements, like the type of sensors and altitude, to ensure the surveying quality.
This calculator and the accompanying article will help you understand what ground sample distance is.
Ground sample distance
Spatial accuracy is critical for aerial surveys and remote sensing. The ground sampling distance is between the centers of two pixels measured on the ground. In other words, the distance between the objects on the ground is represented by two pixels in the image.
For instance, a picture with a GSD of 1 meter per pixel means that the distance between objects one pixel apart in the image is 1 meter apart on the ground. This parameter sets the resolution of the imagery and survey, helps extract data from the survey results, and is measured in the units of length/pixel.
The ground sample distance depends on the camera and the working distance between the camera and the object. Let's call the working distance altitude in this case. You can calculate the parameter using the equation:
where:
- – Sensor width;
- – Altitude or height of the flight;
- – Focal length (see focal length calculator); and
- – Image width.
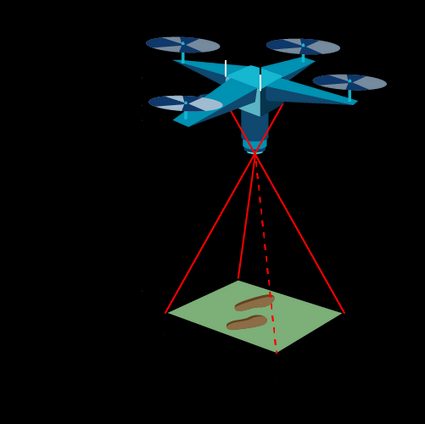
Image size
If you are wondering how much storage a 5000 px image would occupy. We've got you covered with our image file size calculator.
Using the GSD calculator
The GSD calculation helps in mission planning for aerial surveys. For instance, let's calculate the altitude we need to achieve a GSD of 2 cm/px.
Consider a drone with a sensor width of 13 cm fixed with a camera having a focal length of 10.62 mm. Assume the image width to be 5000 pixels.
To calculate the working distance or altitude:
-
Enter the camera's focal length as .
-
Fill in the image width, .
-
Insert the ground sample distance, .
-
Enter the sensor width, .
-
The ground sample distance calculator returns:
This means, the drone must fly at a height 81.7 meters to achieve a resolution of 2 cm/px with the current set of sensors. And that's how you can use this calculator to plan your surveys.
FAQs
What do you mean by ground sample distance?
The ground sample distance is the distance between objects on the ground represented by two pixels. It is measured in the unit of length/pixels. The parameter sets the spatial resolution of the aerial mapping and surveying process.
How do I calculate ground sample distance?
To calculate the ground sample distance:
- Multiply the sensor width and altitude.
- Divide the product by focal length of the camera.
- Divide the resultant by the image width to obtain the ground sample distance for the image.
How does ground sample distance affect accuracy?
The ground sample distance is directly proportional to accuracy. Lowering the ground sample distance means greater detail in the image. However, this also means the camera is much better quality or the drone is flying at a low altitude.
What is the sensor width to achieve a GSD of 2.5 cm/pixels from 100 m?
The sensor width to achieve a GSD of 2.5 cm/px is 12.5 cm. Considering a drone flying at 100 m altitude having a camera with a focal length of 0.1 m and image width of 5000 pixels, the sensor width is given by:
S = 2.5 × 0.1 × 5000 / 100 = 12.5 cm.