Triangle Scale Factor Calculator

Creators

Luis Hoyos

Luis is a mechanical engineer who works at Omni Calculator as a content creator and researcher specializing in math and physics calculators with a focus on thermodynamics and classical mechanics. With a strong foundation in mechanical engineering, Luis is passionate about creating tools that simplify complex concepts and improve everyday life. Outside of work, Luis likes weightlifting and applying his engineering knowledge to optimize the thermal conditions of his home, all while caring for four beloved cats. See full profile

Check our editorial policy

Reviewers

Arturo Barrantes

Arturo Barrantes is a versatile professional who transitioned from mechanical engineering to finance and then to software development. Currently working as an AWS Senior Developer at Indra, he combines his diverse expertise to create practical financial calculators. Arturo is passionate about financial education in Latin America and has spoken at multiple conferences on personal finance and investment strategies. See full profile

Check our editorial policy

New

If you're searching for how to find the scale factor of a triangle, this scale factor calculator is for you.

With this calculator, you can find the scale factor of similar triangles in two ways:

Checking similarity: This option checks whether two triangles are similar or not, and in case they are, the tool calculates the triangle scale factor. You have to fill in all of the options. You can select between three similarity criteria related to the information known:
- Side-Side-Side (SSS);
- Side-Angle-Side (SAS); and
- Angle-Side-Angle (ASA);
Finding the missing side: If you input the information about the first triangle and one of the sides of the second triangle, the tool will calculate the triangle scale factor and, as a bonus, the remaining dimensions of the second triangle.

How to find the scale factor of a triangle

To know how to find the scale factor of a triangle, first, we must understand what similar triangles are. Two triangles are similar if one of these conditions holds:

Their corresponding sides are in proportion, so one triangle is a scaled version of the other. The scale factor measures the degree to which this occurs.
Two corresponding angles are congruent.

🙋 If one of the above conditions is true, the other one will also be true.

Consider the following two triangles:

ABC and DEF similar triangles. — The sides of $\triangle \text{ABC}$ and $\triangle \text{DEF}$ are proportional.

As the corresponding sides are in proportion, then:

\frac{\text{DE}}{\text{AB}} = \frac{\text{EF}}{\text{BC}} =\frac{\text{DF}}{\text{AC}} = k = 2

Therefore, we can say $\triangle \text{ABC} \sim \triangle \text{DEF}$ , where the symbol $\sim$ indicates that the triangles are similar.

The $k$ term refers to the scale factor. It measures the proportion of similarity between two corresponding sides.

Other tools similar to this triangle scale factor calculator

Now that you know how to find the scale factor of two triangles, you can look at these other exciting tools:

Graphic representing the previous example

FAQs

How do I find the scale factor of two triangles?

To find the scale factor of two triangles, follow these steps:

Check that both triangles are similar.
If they are similar, identify the corresponding sides of the triangles.
Take any known side of the scaled triangle, and divide it by its corresponding (and known) side of the second triangle.
The result is the division equals the scale factor.

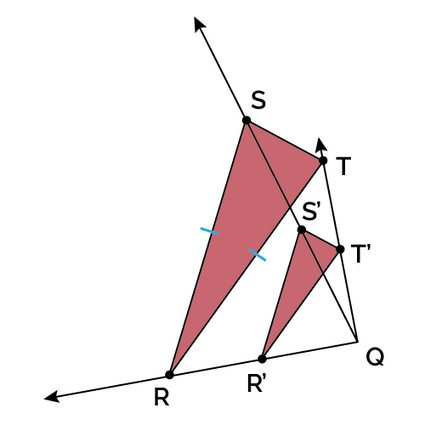
What is the leg length of a triangle RST dilated by a scale factor of 1/2?

If an isosceles triangle RST was dilated by a scale factor of 1/2, and the legs of the dilated triangle (R'S' and R'T') measured 8 units, the length of the legs of the original triangle must be 16 units.