Sequence Calculator

Learn how to calculate sequences of numbers or simply find the values of their term with our versatile tool! Keep reading this article to learn:

• What numerical and integer sequences are;
• The formulas to calculate a sequence's nth term (arithmetic and geometric sequences);
• Interesting integer sequences (prime numbers, Fibonacci numbers, figurate numbers);
• And much more.

We will teach you how to use our versatile tool and give you some examples of sequence calculations. What are you waiting for? Let's start counting!

A numerical sequence is an ordered (enumerated) list of numbers where:

• The order in which the numbers appear matters;
• Repetition is allowed; and
• Each term can be considered the output of a function where instead of an argument, we specify a position.

The terms of a sequence are (usually) represented by the letter $a$ followed by the position (or index) as subscript. Then, the first term of a sequence would be $a_0$, followed by $a_1$. A generic term in position $n$ is $a_{(n+1)}$.

Among many types of sequences, it's worth remembering the arithmetic and the geometric sequences.

Integer sequences

If each term of a sequence is an integer number, then we are dealing with integer sequences. While technically, there's not much difference from any other generic mathematical sequence; we can quickly calculate integer sequences by hand. Many integer sequences are well known. We can quote:

• The Fibonacci sequence;
• The prime numbers sequence;
• The square and cube numbers; and
• Many more.

The arithmetic sequence is, arguably, the most common and straightforward of the mathematical sequences. An arithmetic sequence is a sequence where two adjacent terms differ by the same constant difference. In mathematical terms, we write this definition as:

where $d$ is the constant difference.

You can calculate a sequence defined this way by only knowing an initial value and $d$: repeated subtractions and sums will eventually populate all possible positions.

For this reason, we can easily find the first term of the sequence ($a_0$) if we know the value at position $n$ and $d$, or the n-th terms starting from the first one and $d$. We use this formula, changing the position of the factors according to what we are looking for:

If you plot the terms of an arithmetic sequence, you'll find a straight line that, in the Cartesian coordinates, would have a slope equal to $d$.

In a geometric sequence, two adjacent terms have constant ratio $r$. This ratio is given by the formula:

Using this formula, we calculate the terms of a geometric sequence by simply multiplying (if we are moving forward) or dividing (if you are moving in the opposite direction) a term by $r$:

To calculate the nth term of a geometric sequence starting from the initial term $a_0$, you can start by using the previous formula to calculate the sequences' first terms:

As you can see, the constant ratio can be expressed as a power: $r^2$, $r^3$, and so on. So to calculate the nth term of a geometric sequence, we raise $r$ to the proper exponent:

A geometric sequence can grow extremely fast for constant ratios greater than $1$, closely resembling the behavior of exponential growth.

Number theory and geometry meet in an unexpected way involving the so-called figurate numbers. A figurate number of items can be arranged in a specific geometric shape: a square number of dots, for example, can be arranged in a square. Take $36$, for example:

As you can see, we can arrange $36$ as a square with side $6$.

Square numbers are the most famous figurate number, closely followed by cube numbers. Their sequences are pretty straightforward.

For square numbers, the nth term is:

Similarly, for cube numbers, we have:

The first ten square numbers, starting from $a_0=0$ are:

The first ten cube numbers are:

Notice how quickly the last set grows compared to the former!

Triangular numbers are slightly less common, as they find fewer applications and remain mostly a niche mathematical curiosity. However, we think they are pretty cool, so we included them in our calculator!

The nth term of the sequence of triangular numbers is given by the following formula:

where the second equality introduces the concept of binomial coefficient.

The first set of triangular numbers are:

Maybe it's not evident, but there is a neat relationship between square numbers and triangular numbers. If you consider the same initial term $a_0=T_0=0$, then:

You can see this formula with your eyes:

There are two additional sequences of particular interest in number theory due to their properties and repeated appearances in mathematics. We are talking about prime numbers and Fibonacci numbers.

Prime numbers are numbers divisible only by themselves and by $1$. We can use the ancient Erathostenes's sieve algorithm, but this method is not useful for large terms. Nowadays, it's easy to find tabulated sequences of prime numbers, such as this table of prime numbers up to 1000 billion. Here is a sequence of the first prime numbers

$1$ and $0$ are not prime numbers, even though the former was a matter of a long debate!

Fibonacci numbers can be considered a twisted form of an arithmetic sequence, where the constant difference is not constant: instead, the difference between two adjacent numbers in the Fibonacci sequence is equal to the term right before both of them. In mathematical terms, we write:

which allows us to write the expression for the n-th term:

There is no way to escape this constraint: even to start the sequence, we need to specify two Fibonacci numbers. By convention:

Knowing the first two terms, we can compute the third one:

Yup, repetition is allowed. And while in other instances, this would cause the sequence to repeat itself, after the third term, the numbers of the Fibonacci sequence never repeat. The next terms would be:

The difference between the terms increases, making the Fibonacci sequence almost an exponential one. To learn more about this curious, mathematical sequence, visit our Fibonacci calculator!

Powers of 2

We included another significant sequence in our calculator: the sequence of the powers of 2. This sequence is nothing but a geometric sequence with constant ratio $r=2$ starting at $a_0=2^0=1$.

Even though it's "just" a geometric sequence, with the development of informatics, the powers of two became a staple of our civilization; hence they deserve this appearance!

Factorials

Factorial numbers are interesting numbers where, if we set $a_1=1$, then $a_n$ is equal to the product of all integers between $1$ and $n$. In mathematical terms:

The first factorial numbers are:

Factorial numbers grow pretty quickly! In mathematics, they have an important role in combinatorics, the study of the ways we can arrange objects belonging to a set.

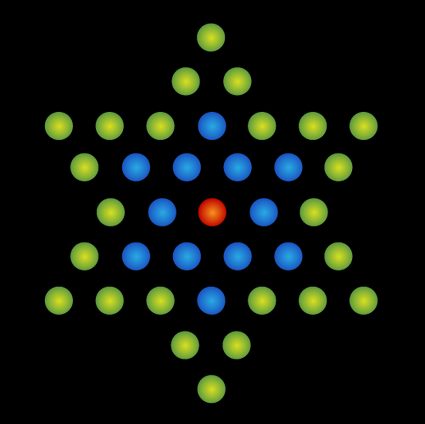
Star numbers

The last sequence you will explore in our number sequence calculator is the star numbers, another class of figurate numbers where each term indicates the size of a collection of items you can arrange in a six-pointed star fashion. There is a neat formula to calculate the nth term of this sequence:

The first star numbers are $1,\ 13,\ 37,...$. Here is a graphical representation of $s_2=37$

Our sequence calculator is a versatile tool. To use it, follow these simple steps:

1. Choose the type of sequence you are interested in: use the drop-down menu at type.

2. Fill the parameters of the desired sequence. What can we ask you?

   • We always ask you the initial position: this is the index of the first term of which you want to see the value. If you input $5$, we will print the terms starting from $a_5$.

   • The first term of the sequence. This can help us find the terms starting at the selected position in the geometric and arithmetic sequence.

   • The constant ratio or constant difference if they appear in the sequence's formula.

3. Once you fill in all the required, we will print the first five terms starting from the selected index.

Don't mistake sequence and series: discover their difference in the sum of series calculator.

The formula to calculate the arithmetic sequence is:

a_n = a₀ + n × d

where:

• a₀ — The first term of the series;
• d — The constant difference between two adjacent terms; and
• n — The position of the nth term.

You can easily derive this formula from the definition of arithmetic sequence:

a_n = a_n-1 + d

where you can substitute a_n-1 recursively:

a_n = a_n-2 + d + d

until you reach the initial term a₀.

To calculate the Fibonacci sequence, follow these easy steps:

1. Define the first term of the sequence: F₀ = 0.
2. Define the second term of the sequence: F₁ = 1.
3. Compute the third term as the sum of the previous ones: F₂ = F₀ + F₁ = 0 + 1 = 1.
4. Repeat the third step until you reach the desired position.

The first Fibonacci numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,....

A number sequence is a sequence of numbers (terms) identified by their position as members of a list. The most famous sequences are the arithmetic sequence and the geometric sequence. Other examples of sequences include:

• The Fibonacci sequence;
• The prime numbers sequence;
• Sequence of square and cube numbers;
• The powers of 2;

and many more.

To find out if a sequence is geometric or arithmetic, you must follow some easy steps:

1. Write down the terms of your sequence. Start choosing pairs of adjacent terms (in the form a_n and a_n+1).

2. Calculate the difference between the adjacent terms in each pair. If the difference is the same for each pair, you are dealing with an arithmetic sequence.

3. If the previous test failed, calculate the ratio between the two pairs of numbers. If it's constant for each pair, then you found a geometric sequence.

a₉₉ = 495, assuming that the first term is zero (a₀ = 0). To calculate this result, we used the formula to calculate the nth term of an arithmetic sequence:

a_n = a₀ + n × d

where we substitute the values:

a₉₉ = 0 + 99 × 5 = 495