Multiplying Fractions Calculator

With this multiplying fractions calculator, you'll quickly learn how to perform multiplication on fractions, be they simple fractions, improper fractions, or mixed numbers. Also, you will learn how to multiply fractions with whole numbers, and even multiplying three fractions won't be a hurdle anymore. Remember, that in our tool you can multiply up to five fractions - awesome, isn't it? 😍

If you'd like to check how other operations on fractions work, take a peek at our versatile fraction calculator.

Multiplying fractions is not rocket science, believe us. You only need to know how to multiply numbers, which you surely do, and how to simplify fractions. This is a bit more involved, but you can quickly learn more with Omni's simplify fractions calculator.

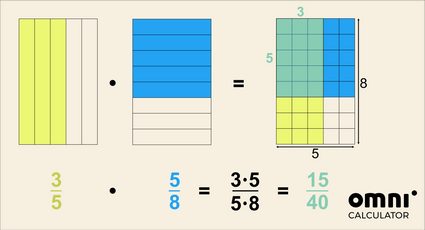
Let's say you have two fractions, 3/5 and 5/8. How to multiply these fractions?

³/₅ * ⁵/₈ = ?

1. Multiply the numerator by the other numerator and the denominator by the other denominator:

   ³/₅ * ⁵/₈ = ^{(3 * 5)}/_{(5 * 8)}= ¹⁵/₄₀

If you had more fractions than two, the process would be analogical: multiply all numerators together to make a new numberator, and do the same with the denominators to get a new denominator.

2. If needed, simplify a fraction:

   ¹⁵/₄₀ = ³/₈

To make a reduction, find greatest common factor of the numerator and denominator, and divide them by that value.

If you'd like to get some visual intuition how multiplying fractions works, take a look at this graphic:

When it comes to multiplying fractions by whole numbers, it's even easier! Why? Remember that you can write every whole number as a fraction, which is equal to that number over 1.

As a word problem, you can imagine it as seven people attending your Halloween party 🎃👻🕷️. You bought three pumpkin pies, and you cut each pie to six equal slices. Now you're wondering if it's enough for everybody, if each of your guests would like to eat two slices of a pumpkin pie 🥧

1. Think about the problem: how to write down one slice of a pie as a fraction? You cut each pie into six, and you're taking one part out of it. So it will be:

   ¹/₆

2. You know that each guest would like to eat two slices. You will have seven guests (let's assume that you're not eating, because you're not a big fan of a pumpkin pie). So you need to multiply 7 (guests) by 2/6 (2 slices out of 6):

   7 🧍 * ²/₆ 🥧

   7 * ²/₆

3. By multiplying a fraction by a whole numbers, we perform the same operation as we did when we multiplied simple fractions: we multiply the numerators by the numerators and the denominators by the denominators. As we wrote before, you may always write a whole number as its number over one:

   7 = ⁷/₁

   Finally:

   7 * ²/₆ = ⁷/₁ * ²/₆ = ^{(7 * 2)}/_{(1 * 6)} = ¹⁴/₆ = 2 ²/₆ = 2 ¹/₃

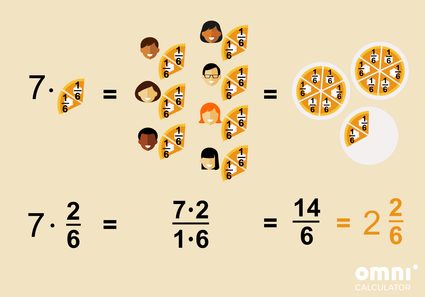
So, lucky you!🍀 You can feed all of your hungry guests with three pies 🥧🥧🥧! Check the result with our multiplying fractions calculator, and have a look at the step-by-step solution if you have any doubts.

Multiplication of mixed numbers is also a no-brainer if you know how to multiply simple fractions. It just needs one additional step at the beginning - a change from a mixed fraction to the improper fraction. You can refresh your knowledge with our improper fraction to mixed number calculator.

Let's say we want to multiply the mixed numbers 2 ³/₅ and 1 ¹/₆

To begin, turn the mixed fraction 2 ³/₅ to its improper fraction:

1. Multiply the denominator by the whole number:

   2 * 5 = 10

2. Add the numerator to the result:

   10 + 3 = 13

   This is the numerator of your improper fraction.

3. The denominator stays the same as in the original mixed number. It's 5 in our example:

   ¹³/₅

Repeat the procedure for 1 ¹/₆. You'll get the mixed number equivalent, in its improper fraction form:

1 ¹/₆ = ^{((6 * 1) + 1)}/₆ = ⁷/₆

Then, multiply the fractions as usual:

¹³/₅ * ⁷/₆ = ^{(13 * 7)}/_{(5 * 6)} = ⁹¹/₃₀

You can also change the result back from an improper fraction to a mixed number:

⁹¹/₃₀= 3 ¹/₃₀

The problem of multiplying fractions with mixed numbers is very similar to the problem we just dealt with - multiplying mixed numbers. This time, one of your fraction is in its simple form, and the other - in its mixed fraction form.

The solution is simple: you need to leave your simple fraction in its current form, and, again, change the mixed fraction to its improper fraction form. Then, following the standard procedure, you'll get the result for multiplying fractions with mixed numbers.

After such a thorough read, we're sure that you know everything about multiplying fractions: how to multiply simple fractions, how to multiply fractions with whole numbers, and how to multiply mixed fractions. So, it's high time to check out how our multiplying fractions calculator works!

Let's choose a scenario we didn't talk about before - we'll try multiplying three fractions:
³/₄, 1 ⁵/₆ and -²/₇. Notice that we're also multiplying fractions with mixed numbers, as we have one fraction in a mixed form. So, how to calculate it with our tool?

1. Choose the type of fractions. As you have one fraction in a mixed form, pick that option.
2. Input the data:

• For the first fraction, leave the whole number box empty (or enter 0), enter 3 into the numerator field, and 4 into denominator one;
• For the second fraction, input 1 as the whole number, 5 as the numerator, and 6 as the denominator; and
• For the third fraction, leave the whole number field empty again, put -2 in the numerator box, and 7 in the denominator box.

3. And that's it, the multiplying fractions calculator will show you the result of the multiplication of three fractions! It's -¹¹/₂₈.
4. To understand the process, check out the step-by-step solution.

Let's analyze another example: the multiplication of the fraction ⁷/₈ by 13, which is a whole number, of course.

1. Pick the type of fraction from the drop-down list. Choose mixed form, as you'll need the whole fraction part.

2. Enter the fractions:

   • The first numerator is 7, and the denominator is 8 (the whole part is left empty)
   • In the whole part of second fraction, enter 13 and leave the fractional part empty

3. The multiplying fractions calculator displays the result: ⁹¹/₈, which is 11 ³/₈ in its mixed number form. Easy-peasy!

You can also use the simple fraction form as well, by changing your whole number to ¹³/₁ 😎