LFSR Calculator

Generating random numbers on a deterministic machine like a computer is complicated — this is where linear-feedback shift registers (LFSR) come in handy, and you can try them out with our LFSR calculator. With a little bit of math and some computer science knowledge, you will learn everything you need about this special type of register.

Here we will guide you through the many questions you might have, like:

• What an LFSR is;
• Fibonacci LFSR vs Galois LFSR;
• How an LFSR works;
• The applications of linear-feedback shift registers; and
• How to use our LFSR calculator.

First: what is a shift register? It's a type of electronic logic circuit that stores and transmits data by moving one bit in a particular direction of a register at every step: a basic type of computer memory. We already have a bit shift calculator that talks about this principle — go check it out!

Long story short, a shift register is a series of flip-flops connected in a sequential fashion. Every flip-flop corresponds to a bit of memory (they are at the base of every digital memory in use today). In a shift register, the output of each flip-flop is the input of the next one. There are various types of shift registers — the type most commonly used sees the output bit of the register being also the input bit of the next cycle. This is the basis of digital memories.

If you ask a computer scientist what a flip-flop is, they likely won't tell you "a type of summer shoes" — not because they don't spend time outside, but because computer memory is based on an element with the same name. A flip-flop is a circuit with two stable states (bistable): if we call them 1 and 0, it is straightforward to see why they are so valuable for computing. It consists of an input, a pair of complementary outputs (if one of them outputs 1, the other one outputs 0) and a reset. Flip-flops can store one bit of memory, either outputting 0 (low) or 1 (high). When triggered by the input, the circuit switches to the high state until a signal from the reset moves it back to the low state.

If the input bit (the bit entering the register) of the current state of the shift register is the result of some linear operation of the previous state, then we have a linear-feedback shift register or LFSR.

The logic gates XOR (exclusive or) and NXOR (its negation) are the two linear functions used in LFSR: one is the one's complement of the other, meaning that the math underlying is almost the same.

Here is the truth table for the XOR gate. As you can see, it corresponds to calcualte the bitwise binary addition operation (modulo 2 addition) — this will make things easier to understand for sure.

If you want to learn more about binary operations, check our related calculators! They are not strictly bitwise, so that the output can be different than just 1 and 0, but also 10, 11, etc... Try the binary addition calculator or its sibling, the binary subtraction calculator.

To define an LFSR, it is necessary to specify the bits used as arguments in the linear operation: their positions are called taps. In mathematical terms, they correspond to a vector of 0s and 1s, with 1s in the positions of the desired taps.

The register's initial state is called seed, and it highly affects the outcome of the operations of the LFSR.

The output of an LFSR is a sequence of bits (0s or 1s) that are "collected" at the end of the register. The sequence depends on the chosen function and the type of LFSR, but it always obeys specific rules.

It is periodic (unless the register collapses into the null vector, which consistently transforms to itself) with a maximum number of steps to return to the initial configuration equal to $2^n-1$, where $n$ is the length of the register. This number is called the period of the LFSR.

As said before, if the sequence collapses in the null vector, there it remains with trivial periodicity. In that case, the register is not considered an LFSR, and $0,0,...,0$ is not allowed as a seed.

There are two main types of LFSR:

• Fibonacci LFSR; and
• Galois LFSR.

Each of them is defined using the same set of objects, but they differ in how such objects are used.

Fibonacci LFSR

In the case of the Fibonacci LFSR, the value of the bits specified by the taps is summed using XOR operations, resulting in a final value that then becomes the new input of the shift register. On the "opposite side" of the register, the last bit becomes part of the output.

In mathematical terms, we can use a set of two formulas to describe the behavior of a Fibonacci LFSR. Let's introduce the symbols in the formulas: $\vec{X} = [X_1, ..., X_n]$ is the shift register itself. It is a vector with elements $X_{i} \in \{0, 1\}$ (i.e., either $1$ or $0$).

The taps are specified by the vector of the connection coefficients, noted as $\vec{c} = [c_1, ..., c_n]$. Both of these vectors have length $n$. We defining the element-wise product of the register and the connection coefficient vectors as $\vec{Y}$ with elements $Y_i=c_i X_i(t)$. The register at the LFSR obeys the rules:

Where $\oplus$ is the XOR operation or binary addition.

As you can see, we shift the register in the first equation, "ejecting" $X_{n}$ at the time $t$, thus creating the $\vec{X}$ vector at the $t+1$ state, with an empty space in the first position.

The second equation is how we build that first element: a binary addition of all the elements of $\vec{X}$ at the time $t$, multiplied by the corresponding connection coefficients, that are equal to $1$ only in correspondence of the taps.

To "start" the register, we need to feed it a seed, an initial value on which we first apply the rules of the LFSR. The same holds for a Galois LFSR, but the operating principle differs. Let's take a look!

Galois LFSR

In a Galois linear-feedback shift register, we first have to shift every bit that is not a tap to the right. This causes the rightmost bit to be "ejected" and moved to the input.

But this is not all for the output bit. It is also added to each tap before the result moves to the space to the right.

This causes the register to shift unchanged if the output bit is $0$, taking as new input $0$, while in the case of output bit $1$, the tap bits switch, then the register moves to the right. In this case, the input bit is $1$.

The two types of LFSR produce the same result — minus a reflection and a translation — when the taps are the ones generating a maximally long LFSR. In such a register, all possible states are visited — except the null state, which would make the register collapse in a sequence of 0s. The seed choice is not relevant since it would introduce only a shift in the output.

In order to obtain this kind of coupled outputs, the taps of the Galois register must be the counterparts of the ones of the Fibonacci register. We mean that if the taps of the latter are

$1,4,6,12$

which translates to

$1,0,0,1,0,1,0,0,0,0,0,1$,

then the taps we need to use are

$1,7,9,12$

for a Galois LFSR. The transformation is clear when we look at the corresponding vector:

$1,0,0,0,0,0,1,0,1,0,0,1$

Let's see an example of a linear-feedback shift register in action.

First, consider a Fibonacci type. The initial state is $1001$, while the taps are $1101$. Here we mark both output and taps on the initial state:

Now we need to add modulo 2 the "tapped" bits. $1\oplus 0\oplus 1=0$, and thus the new input bit is $0$:

And repeat these operations!

Now take a break: the next state of the register would be $1001$, which is equal to the initial state: from now on, the states would repeat, cycling indefinitely.

The sequence we found is $1001011$, with period 7. It would expand this way: $10010111001011100...$

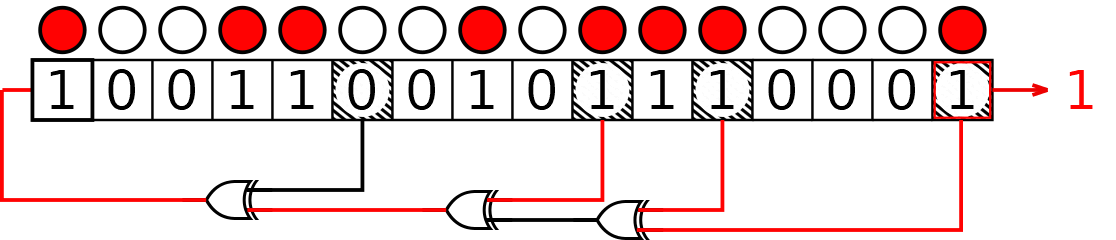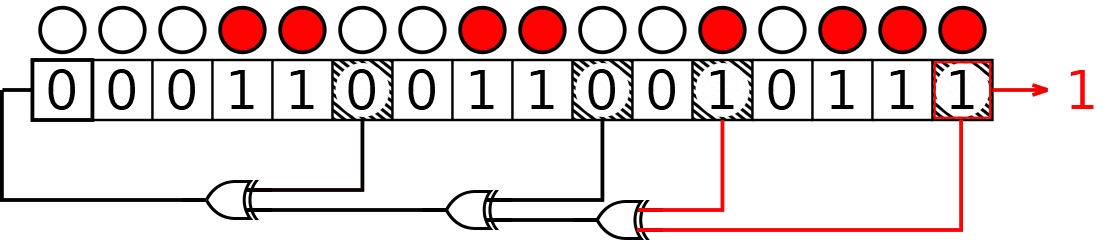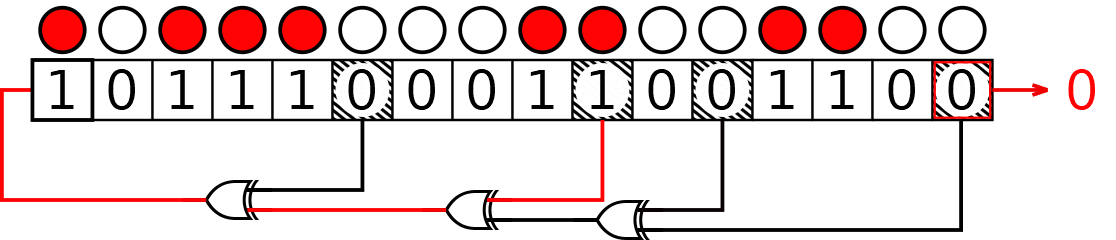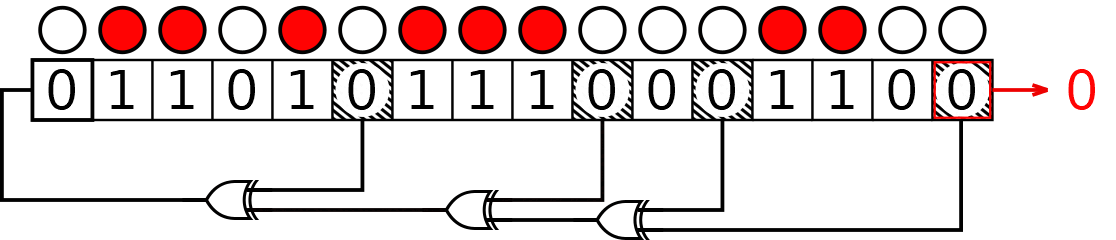
Do you want to try the same example but with Galois LFSR? We got your back!
Remember: initial state $1001$, taps $1101$.

The first output would be $1$: it means we are in for a change. Let's see how the register behaves at the next step.

The second step has $0$ as output. No changes in the register, just a shift:

Repeat those steps, and let's see what happens.

Stop! See the last state? It's the same as the initial state, so we reached the end. This is another period 7 register, with output $1010011$.

You can use our LFSR calculator to find out many things about a selected LFSR. Here we will guide you through it!

First, you have to insert the seed and the taps. Make sure that they have the same length.

Then, choose the type of LFSR you want to use for your register: either Fibonacci or Galois. Choose the desired kind of output too:

• Output: this will show you the sequences of output bits. To make it easier to read, we separated the string into groups of 8 bits.
• Steps: the calculator will give you the detailed iterations of the register.
• Period: you will only get the number of steps repeated in the output.

The last field allows you to specify the desired length of the output/steps you need, but it won't affect the period calculation. If that value is undefined, the calculator will cut the sequence at the end of the first period.

While using our LFSR calculator, you may encounter messages that help you understand the behavior of the register you are using.

For example, if you inserted the correct set of taps, you may find a maximally long LFSR, which means that the period of the LFSR is maximum (equal to $2^n-1$, where $n$ is the length of the register). We will tell you when you are doing so, since they are particularly interesting. You can find tables with the taps for such sequences online, like in this file: these "special taps" correspond to the exponents of characteristic polynomials. Place the tap in the position marked by the exponent (if you see $x$, place a $1$ in the first position).

If you accidentally end up with a null register, we will stop the calculator and let you know. Change your numbers and try again.

Just for fun, let's try it with a mirroring output. Choose a maximally length taps sequence, like $01001$, and a random seed, $11011$. Insert them in our LFSR calculator.

Select "Fibonacci" and "output": the result is

$11011000\ 11111001\ 10100100\ 0010101$

Now switch to "Galois":

$11000110\ 11101010\ 00010010\ 1100111$

We need to reverse it — let us do that for you!

$11100110\ 10010000\ 10101110\ 1100011$

Now let's find the correct shift. Maybe look for a group of clustered $1$s or $0$s, like...

$11011000\ \textcolor{red}{11111}001\ 10100100\ 0010101$

In the Galois output, the same cluster is broken between the end and the beginning of the sequence:

$\textcolor{red}{111}00110\ 10010000\ 10101110\ 11000\textcolor{red}{11}$

Shifting the Galois output ten times to the right, we would find the same output of the Fibonacci LFSR.

Now you should know what a LFSR is and how a LFSR works.

LFSR, shift registers, and flip-flops are all parts of a computer we never see, yet they allow for such a complex machine to function as we know it. Go to our Hamming codes calculator if you want to learn more about how computers work behind the keyboard and monitor!

Try our LFSR calculator in all the possible ways and discover which sequences are the longest or which taps give the maximally long outputs!

LFSRs are shift registers that apply linear operations to their bits according to a certain set of rules. There are two types of LFSRs: Galois and Fibonacci. They differ in the way they perform the operation.

LFSR are used in cryptography to generate pseudo-random numbers and in circuit testing to create sequences containing all possible inputs for a given n-bit register. The (almost) random nature of the output of an LFSR allows the simulation of noise in signals and helps overcome interference in signal transmissions.

The taps of a linear-feedback shift register are the bits that are effectively used in the linear operation. They can be specified as a binary vector. In some instances, they correspond to a maximal-length LFSR, a sequence of all the possible states of the register.

Computers are intrinsically deterministic (only when a physical phenomenon acts on them, it is possible to have a non-deterministic behavior): this makes it difficult to generate truly random numbers on them. Mathematicians developed algorithms that generate sequences of numbers that resemble their random counterparts but are entirely defined by an initial value: the seed.

In order to calculate a Fibonacci LFSR, add the bits in the register marked by the connection coefficients, modulus 2, and consider the result as new input in the register. The last value exits as an element of the output.

In a Galois LFSR, shift every bit to the right if the output bit is zero, and use 0 as new input bit too. If the output bit is 1, all of the bits are shifted to the right, but the ones marked by the taps must switch from 1 to 0 and vice-versa. In this case, the next input is 1.