Last updated: Jul 25, 2024

Isosceles Right Triangle Hypotenuse Calculator

Q: Are right triangles isosceles?

No, right triangles are not usually isosceles. There is only one instance where a right triangle is an isosceles triangle. In this instance, two interior angles are congruent and equal to 45 degrees.

Created by Adena Benn

Adena Benn

LinkedInWebsite

Adena Benn is an Information Technology teacher with a degree in Computer Science. She has been teaching high schoolers since 1996 and loves everything computers. She loves problem-solving, so creating calculators to solve real-world problems is her idea of fun. She writes children's stories, is a seamstress, and is an avid reader. In her spare time, she travels and enjoys nature. See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

What is an isosceles right triangle?How to find the hypotenuse of an isosceles right triangle How to use our isosceles right triangle hypotenuse calculator Looking for more calculators like this?FAQs

Are you on the market for an isosceles right triangle hypotenuse calculator? Then look no further. Our isosceles right triangle hypotenuse calculator will help you to find the length of the hypotenuse.

Keep reading to learn:

What an isosceles right triangle is;
The formula for the hypotenuse of an isosceles right triangle;
The characteristics of the angles of the isosceles right triangle; and
How to use our isosceles right triangle hypotenuse calculator.

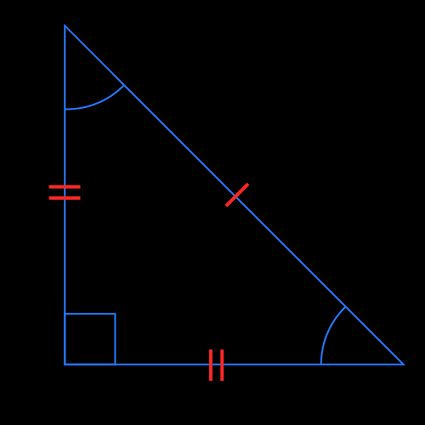
What is an isosceles right triangle?

An isosceles right triangle is a right angle triangle with two equal sides and two equal angles. Because two sides are equal, and one of its interior angles is equivalent to 90 degrees, it is considered both an isosceles and a right-angle triangle.

The interior angles of all triangles add up to 180 degrees. So since we already know that one angle of this triangle is 90 degrees and the other two angles are equivalent, this means that the other two angles are both equal to 45 degrees. In fact, the only isosceles triangle that is also a right angle triangle is one where the other two interior angles measure 45 degrees.

How to find the hypotenuse of an isosceles right triangle

The Pythagoras theorem is the formula used to find the hypotenuse of an isosceles right triangle.

The Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the square of the other two sides. So if the hypotenuse is labeled $A$ and the other two sides are $B$ and $B$ , then using Pythagoras theorem, the formula would look like this:

A² =B² + B²

🙋 Note: Because we know that the other two sides of this isosceles right triangle are equal, we use the same variable to represent them.

So when we work out this equation, we get:

Step 1:

A^2 = 2B^2

Step 2:

A = \sqrt{2}B

Step 3:

A=B × \sqrt{2}

So if we know the measurement of the two equal sides is 5 cm, the hypotenuse would be:

A = 5 × \sqrt{2}

So:

A = 7.071

Of course, you may skip the formula altogether, and use our isosceles right triangle hypotenuse calculator to get the job done effortlessly 😉.

How to use our isosceles right triangle hypotenuse calculator

To use our isosceles right triangle hypotenuse calculator:

Enter the measurement for B, the two equal sides.
The measurement for A, the hypotenuse, will be generated for you.

Looking for more calculators like this?

Here is a list of related calculators:

FAQs

Are right triangles isosceles?

No, right triangles are not usually isosceles.

There is only one instance where a right triangle is an isosceles triangle. In this instance, two interior angles are congruent and equal to 45 degrees.

How to find the hypotenuse of an isosceles right triangle?

We use the following steps to find the hypotenuse of an isosceles right triangle.

Using the Pythagoras theorem: The square of the hypotenuse A is equal to the sum of the square of the two equal sides B:

A² = B² + B²
Add the square of the two equal sides:

A² = 2B²
Find the square root of the two equal sides:

A = B × √2.
The answer generated is the length of the hypotenuse.