Last updated: Jul 08, 2024

Inscribed Angle Calculator

Q: What is the inscribed angle if the central angle is 45°?

The inscribed angle is 22.5° . To arrive at this answer yourself, follow these steps: Divide the central angle by 2 to get 45°/2 = 22.5° . Verify this answer with our inscribed angle calculator.

Q: What is the angle inscribed by the two ends of a diameter?

The angle inscribed by the ends of a diameter is always a right angle . You can verify this with the inscribed angle theorem , too! Since the central angle subtended by the two ends of a diameter will be 180° , the inscribed angle will be half of 180°, equal to 90° .

Created by Krishna Nelaturu

Krishna Nelaturu

Krishna holds a Master's degree in Applied Mechanics and never shies away from asking questions and digging deeper. He has two years of experience in steel castings and a particular fascination for vehicle dynamics. For his thesis, Krishna developed a new optimization method to reduce squeak and rattle in premium cars. He is passionate about mathematics and physics and constantly wonders about our place in the Universe. He also loves stories and storytelling and hopes to write a book someday. See full profile

Check our editorial policy

Reviewed by Luciano Miño

Luciano Miño

Physics bachelor student with 4+ years of experience as a web developer and tutor for high school and college students. Passionate about physics, programming, and video games. While he doesn't have all the answers, he'll search high and low to get one if it means helping someone or learning something new. See full profile

Check our editorial policy

New

Table of contents

What is an inscribed angle?Inscribed angle theorem - Inscribed angle formula Calculating central angle, inscribed angle, and arc length Using this inscribed angle calculator FAQs

Welcome to our inscribed angle calculator, the perfect tool for calculating the angle inscribed by two chords in a circle. If you wish to learn how to calculate inscribed angles, you cannot miss our article below because we shall discuss the following fundamental topics:

Inscribed angle theorem;
Calculating central and inscribed angles;
Calculating arc length from the inscribed angle and vice versa; and
Some frequently asked questions.

What is an inscribed angle?

An inscribed angle $\theta_i$ is the interior angle formed by two chords intersecting on a circle. The angle subtended at the circle's center by the endpoints of these chords is known as the central angle $\theta_c$ .

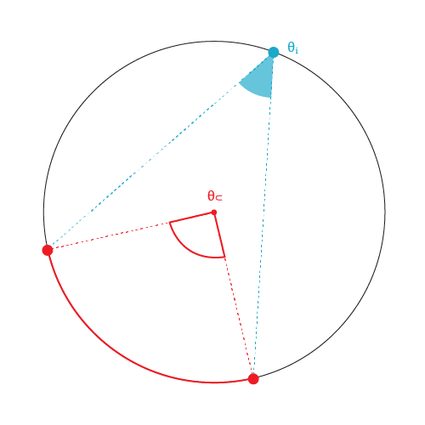
Inscribed angle and central angle subtended by the same arc on a circle. — Inscribed angle $\theta_i$ and central angle $\theta_c$ . The arc length (marked in red) is vital for central angle calculation.

🔎 If you wish to delve deeper into calculation methods of the central angle, visit our central angle calculator!

Inscribed angle theorem - Inscribed angle formula

The inscribed angle theorem establishes a relationship between the central and inscribed angles. It states that:

The inscribed angle is equal to half of the central angle; and
Changing the vertex of the inscribed angle does not change the angle so long as the vertex remains on the circle's circumference.

From this theorem, we get a simple formula for the inscribed angle:

\theta_i = \frac{\theta_c}{2}

Where:

$\theta_i$ - The inscribed angle; and
$\theta_c$ - The central angle.

For example, if the central angle is $120 \degree$ , the inscribed angle would be:

\theta_i = \frac{\theta_c}{2} = \frac{120}{2} = 60 \degree

Calculating central angle, inscribed angle, and arc length

We now know how to calculate the inscribed angle from its central angle. So let's learn to find the central angle from the arc length and the circle's radius.

The formula for the arc length subtending the central angle $\theta_c$ is given by:

L = \theta_c \cdot r

Where:

$L$ - Arc length;
$\theta_c$ - Central angle in radians; and
$r$ - Circle's radius.

Are you intrigued to learn more about the arc length? Head to our arc length calculator!

If you're burning with the question how to calculate the arc length with an inscribed angle, we shall combine the above relation with the inscribed angle formula to obtain the following:

L = 2 \cdot \theta_i \cdot r

⚠️ Make sure the angles are in radians before using the arc length formula!

For example, if the inscribed angle in a $2 \text{ m}$ circle is $45 \degree$ , let's calculate its arc length:

Convert the inscribed angle into radians:

\qquad 45 \degree = 45 \times \frac{\pi}{180} = \frac{\pi}{4} \rm{rad}

Use the arc length formula from the inscribed angle:

\qquad \begin{align*} L &= 2 \cdot \theta_i \cdot r\\ &= 2 \times \frac{\pi}{4} \times 2\\ L &= \pi \text{ m} \approx 3.14 \text{ m} \end{align*}

Using this inscribed angle calculator

Our inscribed angle calculator is straightforward to use:

Enter the central angle, and our calculator will find the inscribed angle for you.
Alternatively, enter the radius and arc length, and our calculator will find the inscribed and central angles for you.
Interested in the value of the arc length instead? Our calculator can do that too! Enter the values for the inscribed or central angle along with the circle radius, and the calculator will do the rest!

See how the inscribed angle theorem has simplified the calculation for you? There are other circle theorems that can make your life easier! Head to our circle theorems calculator to learn more about them!

FAQs

What is the inscribed angle if the central angle is 45°?

The inscribed angle is 22.5°. To arrive at this answer yourself, follow these steps:

Divide the central angle by 2 to get 45°/2 = 22.5°.
Verify this answer with our inscribed angle calculator.

What is the angle inscribed by the two ends of a diameter?

The angle inscribed by the ends of a diameter is always a right angle. You can verify this with the inscribed angle theorem, too! Since the central angle subtended by the two ends of a diameter will be 180°, the inscribed angle will be half of 180°, equal to 90°.