Central Angle Calculator

Have you ever wondered how to find the central angle of a circle? The central angle calculator is here to help; the only variables you need are the arc length and the radius.

Read on to learn the definition of a central angle and how to use the central angle formula.

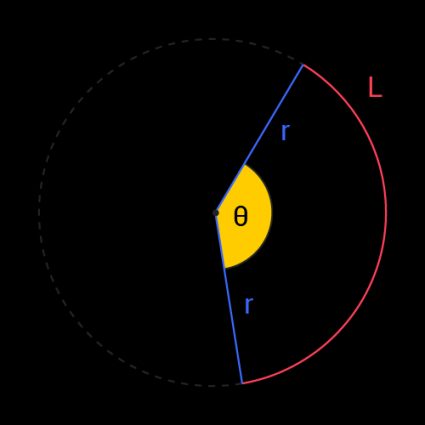
A central angle is an angle with a vertex at the center of a circle whose arms extend to the circumference. You can imagine the central angle being at the tip of a pizza slice in a large circular pizza.

You can find the central angle of a circle using the formula:

θ = L / r

where θ is the central angle in radians, L is the arc length, and r is the radius.

The simplicity of the central angle formula originates from the definition of a radian. A radian is a unit of angular size, where 1 radian is defined as a central angle (θ) whose arc length is equal to the radius (L = r).

Because maths can make people hungry, we might better understand the central angle in terms of pizza. Believe it or not, but pizzas are great for explaining the math of a circle, as you can see at our pizza size calculator What would the central angle be for a slice of pizza if the crust length ($L$) was equal to the radius ($r$)?

Since the problem defines $L = r$, and we know that $1$ radian is defined as the central angle when $L = r$, we can see that the central angle is $1$ radian. We could also use the central angle formula as follows:

In a complete circular pizza, we know that the central angles of all the slices will add up to 2π radians = 360°. Since each slice has a central angle of $1$ radian, we will need $2\pi / 1 = 2\pi$ slices or $6.28$ slices to fill up a complete circle.

We arrive at the same answer if we think this problem in terms of the pizza crust: we calculate the circumference of a circle is $2\pi r$. Since the crust length = radius, then $2\pi r / r = 2\pi$ crusts will fit along the pizza perimeter.

Now, if you are still hungry, take a look at the sector area calculator to calculate the area of each pizza slice!

Try using the central angle calculator in reverse to help solve this problem. The Earth is approximately 149.6 million km away from the Sun. If the Earth travels about one-quarter of its orbit each season, how many km does the Earth travel each season (e.g., from spring to summer)?

Let's approach this problem step-by-step:

1. Simplify the problem by assuming the Earth's orbit is circular (The Earth's orbit is actually elliptical and constantly changing). In this model, the Sun is at the center of the circle, and the Earth's orbit is the circumference.

2. The radius is the distance from the Earth and the Sun: $149.6$ million km.

3. The central angle is a quarter of a circle: $360\degree / 4 = 90\degree$.

4. Use the central angle calculator to find arc length.

You can try the final calculation yourself by rearranging the formula as:

Then convert the central angle into radians $90\degree = 1.57\ \mathrm{rad}$ (use our angle converter if you don't remember how to do this), and solve the equation:

When we assume that for a perfectly circular orbit, the Earth travels approximately 234.9 million km each season!

To find the central angle of a circle, use the formula:

θ = L / r

where:

• θ — Central angle in radians;
• L — Arc length; and
• r — Radius of the circle.

To find the central angle of a circle, you need to calculate the ratio of arc length to the radius of a circle.

You can imagine the central angle being at the tip of a pizza slice in a large circular pizza.

To find a radius with arc length and central angle, you need to calculate the ratio of the arc length and central angle.