FOIL Calculator

We developed this FOIL Calculator to help you learn the FOIL method (First Outside Inside Last) for multiplying two binomials. In the text below, we explain what the FOIL method is and show you step-by-step examples of how to do multiplication according to the FOIL method.

Please remember that the FOIL method works for binomials only; for multiplying other polynomials, see Omni's polynomial multiplication calculator.

FOIL is a method for multiplying two binomials. Let's recall that a binomial is the sum of two monomials, and a monomial is a product of a number (coefficient) and variable (unknown) raised to a non-negative integer power (neither negative powers nor fractional powers are allowed). For instance:

• 3, x, 3x, x³ are monomials;
• 3 + x, 3x + 3, x³ + 1, 4x³ + x² are binomials.

A binomial whose highest degree is equal to one is called a linear binomial. Of the four binomials listed above, only the first two, i.e., 3 + x and 3x + 3, are linear binomials.

Suppose now that we want to multiply two linear binomials ax + b and cx + d. By the distributive law, we get:

(ax + b) × (cx + d) = ax × (cx + d) + b × (cx + d)

That is, the binomial cx + d is distributed over the addition in the binomial ax + b. Each of the two resulting terms gets further distributed:

ax × (cx + d) = ax × cx + ax × d

b × (cx + d) = b × cx + b × d

So, in the end, we obtain the following:

(ax + b) × (cx + d) = acx² + adx + bcx + bd

Note that, in total, we've applied the distributive property thrice.
This is when the FOIL method enters the stage. The FOIL method allows you to multiply two binomials quickly, that is, without performing all the intermediate steps. In other words, the FOIL method allows you to go from

(ax + b) × (cx + d)

directly to

acx² + adx + bcx + bd

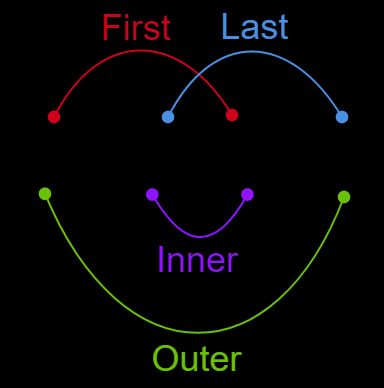
The strange word FOIL is an acronym for the four terms appearing in the final result.

• F ➺ First terms of each binomial are multiplied. That is, the first term of the first binomial and the first term of the second binomial.

• O ➺ Outer terms are multiplied (the terms located at the outermost ends of the binomials). That is the first term of the first binomial and the second term of the second binomial.

• I ➺ Inner terms are multiplied (the middle two terms of the binomials). That is the second term of the first binomial and the first term of the second binomial.

• L ➺ Last terms are multiplied. That is the second term of the first binomial and the second term of the second binomial.

When we've calculated the four partial products (First, Outer, Inner, and Last), there is one last step before we reach the final answer. We need to add the four FOIL terms together. Obviously, the order in which the four terms appear in the sum does not matter and does not need to match the order F-O-I-L.

It was William Betz who came up with the word FOIL in his 1929 text Algebra for Today. He intended it as a mnemonic for students. He wrote: ...first terms, outer terms, inner terms, last terms. (The rule stated above may also be remembered by the word FOIL, suggested by the first letters of the words first, outer, inner, last.)

The FOIL method calculator is really straightforward:

1. Decide whether you need to multiply two linear binomials or binomials of higher degrees.

2. For linear binomials, enter the four coefficients into the FOIL calculator's respective fields.

3. For general binomials, enter the four coefficients and the two exponents into the FOIL calculator's respective fields.

Tip. If your binomial is of the form axⁿ + bx^k, you need to factor out x^min(n,k) so that you get either:

x^k × (ax^{n - k} + b) if n ≥ k

or

xⁿ × (bx^{k - n} + a) if n < k.

Keep in mind the factored term and use the expression in brackets in our calculator. Don't forget about this factored-out term when you write down the final solution!

4. Our FOIL method calculator displays the complete solution along with the steps of the FOIL method.

As the best way to learn the FOIL method is to go through a few examples, let's go ahead and get our hands dirty with three examples:

1. Let's multiply (x + 2) × (3x - 4).

   • First = x × 3x = 3x²
   • Outer = x × (-4) = -4x
   • Inner = 2 × 3x = 6x
   • Last = 2 × (-4) = -8

   The sum of the four above terms is:

   F + O + I + L = 3x² - 4x + 6x - 8

   We can combine the middle two terms, -4x + 6x = 2x, so the final answer is:

   (x + 2) × (3x - 4) = 3x² + 2x - 8.

2. Let's multiply (-2x + 1) × (x³ + 7).

   • First = -2x × x³ = -2x⁴
   • Outer = -2x × 7 = -14x
   • Inner = 1 × x³ = x³
   • Last = 1 × 7 = 7

   The sum of the four above terms is:

   F + O + I + L = -2x⁴ - 14x + x³ - 7

   No simplification is possible, so the final answer is:

   (-2x + 1) × (x³ + 7) = -2x⁴ + x³ - 14x - 7

3. Let's multiply (x² + x) × (2x³ + 7x²).

   • First = x² × 2x³ = 2x⁵
   • Outer = x² × 7x² = 7x⁴
   • Inner = x × 2x³ = 2x⁴
   • Last = x × 7x² = 7x³

   The sum of the four above terms:

   F + O + I + L = 2x⁵ + 7x⁴ + 2x⁴ + 7x³

   Simplifying 7x⁴ + 2x⁴ to 9x⁴, we arrive at the final answer:

   (x² + x) × (2x³ + 7x²) = 2x⁵ + 9x⁴ + 7x³

As we've explained above, the FOIL method helps you to multiply two binomials. In other words, it takes two binomials and returns the sum of four monomials (or fewer than four, if simplifications are possible). The reverse process would be to convert the sum of some monomials into the product of two binomials. Such a process is called factorization.

In particular, the reverse FOIL method aims at factoring a quadratic trinomial, i.e., a polynomial of the form ax² + bx + c, into the product of two linear binomials. However, in contrast to the FOIL method, which is 100% reliable and never fails, the reverse FOIL method works by trial-and-error: we try to guess the First and Last terms of the two linear binomials based on the values of ax² and c so that the sum of the Outer and Inner products equals bx. Let's see an example.

Example

Write the quadratic trinomial 3x² - 2x - 8 as the product of two linear binomials.

We want to find a, b, c, d such that:

3x² - 2x - 8 = (ax + b) × (cx + d)

First we deal with the term 3x². We have 3x² = ax × cx. Note that we can write 3x² as the product of x and 3x, so we make a guess that a = 1 and c = 3. Hence, we have the First terms:

3x² - 2x - 8 = (x + b) × (3x + d)

Next, -8 = b × d and -8 can be written as the product of two numbers in lots of different ways. Let's concentrate on integer factors. We have the following possibilities:

• -8 = 1 × (-8)

• -8 = -1 × 8

• -8 = 8 × (-1)

• -8 = -8 × 1

  as well as

• -8 = 4 × (-2)

• -8 = -4 × 2

• -8 = 2 × (-4)

• -8 = -2 × 4

One by one, we will plug these pairs of values into our binomials as the Last terms and see whether the sum of Outer and Inner terms produces -2x:

• For (x + 1) × (3x - 8) we have Outer + Inner = x × (-8) + 1 × 3x = -5x.

• For (x - 1) × (3x + 8) we have Outer + Inner = x × 8 + (-1) × 3x = 5x.

• For (x + 8) × (3x - 1) we have Outer + Inner = x × (-1) + 8 × 3x = 23x.

• For (x - 8) × (3x + 1) we have Outer + Inner = x × 1 + (-8) × 3x = -23x.

Hmm, nothing works. Let's check the other four possibilities:

• For (x + 4) × (3x - 2) we have Outer + Inner = x × (-2) + 4 × 3x = 10x.

• For (x - 4) × (3x + 2) we have Outer + Inner = x × 2 + (-4) × 3x = -10x.

• For (x + 2) × (3x - 4) we have Outer + Inner = x × (-4) + 2 × 3x = 2x.

• For (x - 2) × (3x + 4) we have Outer + Inner = x × 4 + (-2) × 3x = -2x.

So to get -2x, we need to set b = -2 and d = 4. Finally, we have our answer:

3x² - 2x - 8 = (3x - 4) × (x + 2)

To learn more about factorizing quadratic trinomials, check out Omni's dedicated factoring trinomials calculator or the quadratic equation calculator.