Ellipsoid Volume Calculator

Are you looking for an ellipsoid volume calculator? You've just found the perfect place! We're going to compute the volume of an ellipsoid and give you a step-by-step solution so that you can learn how to do it yourself.

Follow the article below and discover the ellipsoid volume formula, the ellipsoid shape properties, and other useful pieces of information.

An ellipsoid is a surface that might be obtained by "squeezing" a typical ball. It's similar to the American football ball with smoothed corners. 🏈 What's interesting is all the cross-sections of an ellipsoid are in the shape of an ellipse.

We define ellipsoids with the use of semi-axes — line segments that start at the very center of the ellipsoid and finish at the point tangent with the surface (you can think of it the same way as you do about the radius of a circle). We can distinguish three types of semi-axes:

Based on an ellipsoid's cross section (ellipse):

• Semi-major axis — the biggest one; and
• Semi-minor axis — an axis at right angles to the semi-major axis.

3D modification:

• Third axis is at right angles to the two proceeding axes.

All three semi-axes meet at the center of the ellipsoid

Why do we need the ellipsoid volume? 🤔 This shape is pretty common in nature. It's usually used in medicine, in order to estimate the volume of different organs, such as:

• Ovaries;
• Prostate; or
• Urinary bladder.

The ellipse itself is also used in calculating the movements of the planets (see our orbital velocity calculator).

Our ellipsoid volume calculator is simple to use and consists of two main steps:

1. Find the lengths of all three axes of your ellipsoid.

   All of them need to be at 90° (right angles) to each other.

2. Enter the obtained values and enjoy your result! 🎉

We'll display the ellipsoid volume formula, as well as our solution — in all the possible units your heart may desire!

Are you all ready to go? You may also try our all-shapes volume calculator or the sphere volume calculator. 🌎

We can calculate the volume of an elliptical sphere with a simple and elegant ellipsoid equation:

Volume = 4/3 × π × A × B × C

where:

• A, B, and C are the lengths of all three semi-axes of the ellipsoid.

This section will show you how you can designate the ellipsoid using two different methods.

We need to use the Cartesian coordinate system in three dimensions (x, y, z). Then, we need to set the origin of the coordinate system (0, 0, 0) as the center of the ellipsoid.

1. Use the values of the semi-axes:

   Find these three points in the coordinate system:

   • (A, 0, 0)
   • (0, B, 0)
   • (0, 0, C)

   These are the points of the surface that constitute the border of your ellipsoid.

2. Use the ellipsoid formula:

   1 = (x²/A²) + (y²/B²) + (z²/C²)

   This equation is also useful if you need to find the value of any of the semiaxes.

In wireless communication, we have a 3D elliptical region (an ellipsoid volume) between the transmitter antenna and the receiver antenna. This region is determined by the distance between the antennas and the frequency of the wireless wave. It is called Fresnel zone and looks like this:

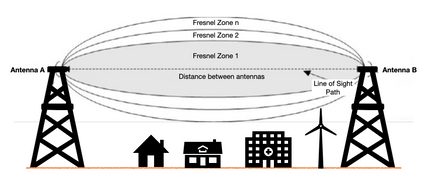
The main ellipsoid volume, called Fresnel zone, has to be kept free in order to secure proper wireless communication. Formulas for determining the space to be kept free are derived from the main ellipsoid equation, as explained here.