Ellipse Area Calculator

The ellipse area calculator will help you determine the area of an ellipse. In the article below, you will find more about the tool and some additional information about the area of an oval, including the ellipse area formula. Read on if you want to learn about the ellipse definition, the foci of an ellipse, and discover what's the ellipse equation. And if you already know all the basics and are looking for something more complicated than this oval area calculator, check out our advanced ellipse calculator.

An ellipse is an oval shape, resembling a squashed circle. It's a generalized case of a closed conical section, which means that you obtain it by slicing a cone with an inclined plane. If the inclination angle equals zero, you get a circle. In fact, circles are a subset of an ellipse!

While talking about the ellipse definition, it's important to mention the ellipse equation, which is as follows (please note that this is not the ellipse area formula!):

where:

• $(x, y)$ — Coordinates of an arbitrary point on the ellipse;
• $(c_1, c_2)$ — Coordinates of the ellipse's center;
• $a$ — Distance between the center and the ellipse's vertex, lying on the horizontal axis; and
• $b$ — Distance between the center and the ellipse's vertex, lying on the vertical axis.

The foci of an ellipse are two points that lie on its longest axis, equidistant from the ellipse's center on each side. You need to determine them if you want to draw an oval. The foci on an ellipse definition are the set of all points for which the sum of distances to the first and second focus is equal to a constant value.

In the image above, the foci are points $F_1$ and $F_2$.

To calculate the area of an oval using our calculator, you only need to do two things:

1. Input the $x$ value.
2. Input the $y$ value.
3. Find the result in the bottom-most field of the ellipse area calculator.

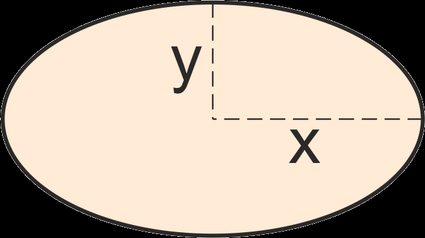
But how does it work? The ellipse area formula is much shorter than the general ellipse equation:

where:

• $X$ — Distance between the center of the ellipse and a vertex; and
• $Y$ — Distance between the ellipse center and a co-vertex.

You can see which distances they are in the illustration above the oval area calculator.

If you need to calculate the areas, perimeters, or different parameters of shapes other than an ellipse, you might find some of our geometry calculators helpful. They include:

• Semicircle calculator — tells you all you need to know about the more unusual shape of a semicircle;
• Latus rectum calculator — calculates the latus rectum for any conic section.