Last updated: Jun 05, 2024

Distance from Point to Plane Calculator

Q: What is the shortest distance from point to plane?

When someone gives us a point and a plane in 3D space, the shortest distance from one to the other is along the line perpendicular to the plane dropped from the point. In other words, it is the magnitude of the normal vector that starts from the given point and ends at the plane.

Q: How do I find the distance from a point to the xy plane?

The distance from the point (a, b, c) to the xy plane is equal to the absolute value of the last coordinate, i.e., to |c| . To see how this follows from the general formula for the distance from a point to a plane, you need to plug in A = B = D = 0 and C = 1 , which gives |C×c| / √(C 2 ) = |C × c| / |C| = |c| .

Q: What is the distance from point (1,1,1) to x+y=0 plane?

The distance is √2 ≈ 1.41 . To get this result, we apply the formula distance = |A×a + B×b + C×c|/√(A 2 + B 2 + C 2 ) with A=B=1 and C=D=0 and a = b = c = 1 . We obtain distance = |1×1 + 1×1 + 0×1| / √(1 2 + 1 2 ) = |2| / √2 = √2 .

Q: What is the distance from plane to space origin?

To compute the distance from the plane Ax + By + Cz + D = 0 to the point (0,0,0) : Compute A 2 + B 2 + C 2 . Take the square root of the number from Step 1. Compute the absolute value of D and divide it by the number from Step 2. That's it! You can verify your result with an online distance from point to plane calculator.

Created by Anna Szczepanek, PhD

Anna Szczepanek

PhD, Jagiellonian University in Kraków, Poland

Website

Holds a Ph.D. degree in mathematics obtained at Jagiellonian University. An active researcher in the field of quantum information and a lecturer with 8+ years of teaching experience. Passionate about everything connected with maths in particular and science in general. Fond of coding, she has a keen eye for detail and perfectionistic leanings. A bookworm, an avid language learner, and a sluggish hiker. She is hopelessly addicted to coffee & chocolate – the darker and bitterer, the better. See full profile

Check our editorial policy

Reviewed by Rijk de Wet

Rijk de Wet

LinkedInWebsite

Holds a Master's degree in Data Science / Industrial Engineering, obtained at Stellenbosch University, South Africa. His research investigates using swarm intelligence to solve data clustering and other optimization problems. Will never refuse an offer to play some board games. See full profile

Check our editorial policy

New

Table of contents

What is the shortest distance from point to plane?Distance from point to plane formulas How to use this perpendicular distance from point to plane calculator?FAQs

Whenever you need to calculate the distance from a point to a plane in 3D space, Omni is here to help. If you are new to the topic of finding the minimum distance from a point to a plane, you can read the article below, where we discuss:

What the shortest distance from a point to a plane is;
The distance from point to plane formula;
How to find the distance from a point to a plane by hand; and
Particular cases, like the distance to the xy plane from a point or the distance from any plane to the space origin.

🙋 If our distance from point to plane calculator is not exactly what you're looking for, check out our distance calculator, which covers the topic of distance in a much broader context.

What is the shortest distance from point to plane?

When someone gives us a point and a plane in 3D space, the shortest distance from one to the other is along the line perpendicular to the plane dropped from the point. In other words, it is the magnitude of the normal vector that starts from the given point and ends at the plane.

💡 Visit Omni's vector magnitude calculator if you need a refresher on that.

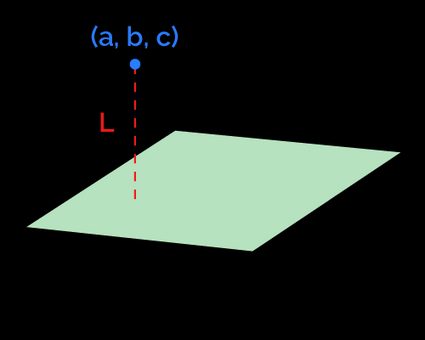
Point and plane with distance between them.

An equivalent explanation that might fancy your imagination may be the following: image a ball centered at the point. We inflate the ball until its surface touches the plane. The radius of this ball is exactly the distance from our point to the plane!

Keep this image in your head, and you'll never forget what the minimum distance from a point to a plane is!

Distance from point to plane formulas

Once we know what the perpendicular distance from a point to a plane means, let's discuss how to calculate it for a given point (a,b,c) and plane. We'll discuss two approaches: when you have the standard form equation of your plane and when you have its normal vector and one point in the plane.

Standard form

Here we assume your plane is given by the equation Ax + By + Cz + D = 0.

The distance between this plane and your point (a,b,c) is.

\footnotesize L = \frac{|A \cdot a + B \cdot b + C \cdot c + D|}{\sqrt{A^2 + B^ 2 + C^2}}

where:

L — Distance;
A, B, C, and D — Coefficients of the standard form plane equation; and
a, b, and c — Coordinates of your point.

What to do if the denominator is zero, you wonder? How do I calculate the distance? Well, you don't. Recall that the condition for Ax + By + Cz + D = 0 to describe a plane in 3D space is that A, B, and C must not all be zero. This translates into A² + B² + C² > 0. So, if it happens that you get zero in the denominator, it means your plane equation is wrong.

Normal vector and a point

Here we assume your plane is given by the normal vector n = [A, B, C] and point p = (x, y, z) belonging to the plane.

To get the formula for distance between this plane (given by n and p) to your point (a,b,c), you first need to derive the standard form plane equation and then apply the formula we've given above. To save you some time, we've done it for you — here's the final formula, ready for you to apply directly to your data:

\footnotesize L = \frac{|A (a\!-\!x) + B (b\!-\!y) + C (c\!-\!z)|}{\sqrt{A^2 + B^ 2 + C^2}}

In this version:

L is the distance;
A, B, C are the coefficients of the normal vector, n;
x, y, and z are the coordinates of the point p belonging to the plane; and
a, b, and c are the coordinates of the point from which you calculate distance.

The condition that A² + B² + C² > 0 corresponds to the fact that the magnitude of the normal vector cannot be zero.

🙋 Need a refresher on vectors? Try our vector calculator!

And that's how we find the distance from a point to a plane. As you can see, these formulas are not very hard, but they are not the simplest as well. Fortunately, our distance from point to plane calculator can perform the calculations for you!

How to use this perpendicular distance from point to plane calculator?

When you want to use our tool to determine the shortest distance from point to plane, you need to:

Input the point's coordinates into the fields a, b, and c.
Decide on how you want to input the plane. You can choose between
- Standard form equation; and
- Normal vector and one point from the plane.
Whatever you choose, input the data into the fields of our distance from point to plane calculator.
Our calculator will display the result immediately.

FAQs

How do I compute the distance from a point to a plane?

To determine the distance from a point to a plane:

Write down the standard form equation of your plane. It should be in the form Ax + By + Cz + D = 0.
Calculate A² + B² + C². If it equals zero, your plane equation is wrong.
Write down the coordinates of the point (a, b, c) from which you want to calculate distance.
Calculate |A×a + B×b + C×c + D|.
Divide it by the square root of the value from Step 2. This is the distance you're looking for!

How do I find the distance from a point to the xy plane?

The distance from the point (a, b, c) to the xy plane is equal to the absolute value of the last coordinate, i.e., to |c|. To see how this follows from the general formula for the distance from a point to a plane, you need to plug in A = B = D = 0 and C = 1, which gives |C×c| / √(C²) = |C × c| / |C| = |c|.

What is the distance from point (1,1,1) to x+y=0 plane?

The distance is √2 ≈ 1.41. To get this result, we apply the formula distance = |A×a + B×b + C×c|/√(A² + B² + C²) with A=B=1 and C=D=0 and a = b = c = 1. We obtain distance = |1×1 + 1×1 + 0×1| / √(1² + 1²) = |2| / √2 = √2.

What is the distance from plane to space origin?

To compute the distance from the plane Ax + By + Cz + D = 0 to the point (0,0,0):

Compute A² + B² + C².
Take the square root of the number from Step 1.
Compute the absolute value of D and divide it by the number from Step 2.
That's it! You can verify your result with an online distance from point to plane calculator.