Coin Rotation Paradox
The coin rotation paradox is a simple yet intriguing example of how a reference frame can bend our perception! In this article, we will explore this entertaining paradox. Keep reading to learn:
- What the coin rotation paradox is.
- Where an extra rotation comes from — the coin rotation paradox explained.
- A generalized and mathematical proof of the coin rotation paradox.
What are you waiting for? Go fetch two identical coins and start experimenting with us!
What is the coin rotation paradox? Definition of the coin rotation paradox
Take two identical coins, and place them side by side. Identify the point of contact, and rotate one around the other, without slipping. When you return to the starting point, how many rotations did the moving coin complete? The answer is two.
How? After all, the point covered a distance equal to the coin's circumference; where did it find the space to add another complete rotation? The answer is simple: keep reading! In the next section, we will shed light on the mystery.
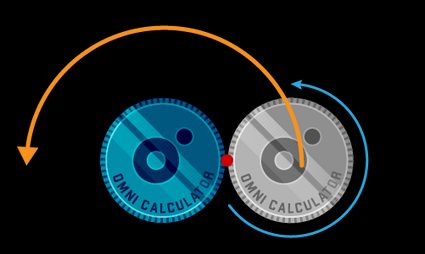
The coin rotation paradox step-by-step
To explain the coin rotation paradox, we need to understand what happens during the coin rotation: start by considering only the first half of the rotation: it will be enough! We will stop when the rotating coin is on the other side of the fixed one. How do you expect to find the coin? Upside-down? Surprise: it has the same orientation as the one at the starting point: hence, it completed a rotation after a single turn!
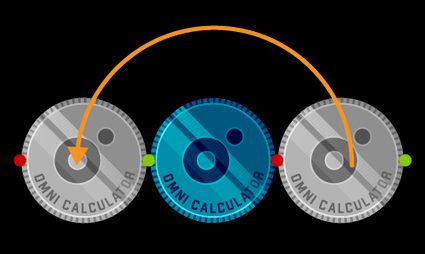
How come? Let's "flatten" the path and see if we can get some insights.

Wait, did you see this? If we unwrap the path, the coin is upside-down after a length of (half the circumference), while we expected it to be with the same orientation. What happened? The answer is rotation. What the coin did by rolling on the flat is half a rotation: , as you can see. It appears upside-down because it rotates only for half of a complete angle.

When we bend the path, adapting it to the half-circle corresponding to half the coin, we add another half rotation, this time not performed "actively" by the coin but characteristic of the shape of the path on which it is moving.
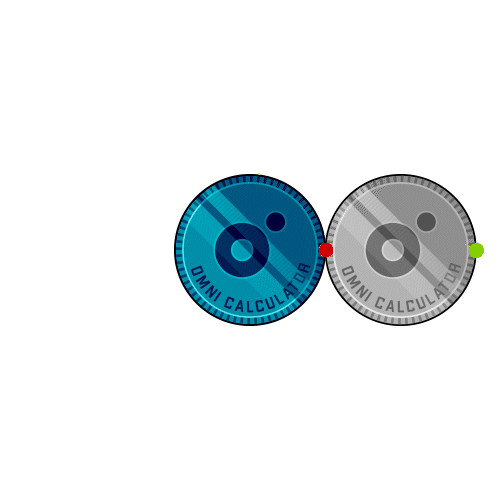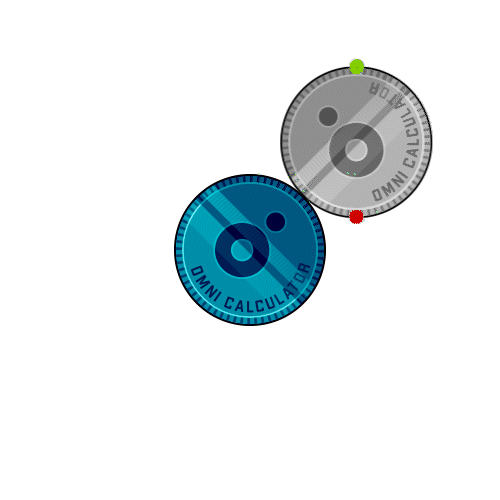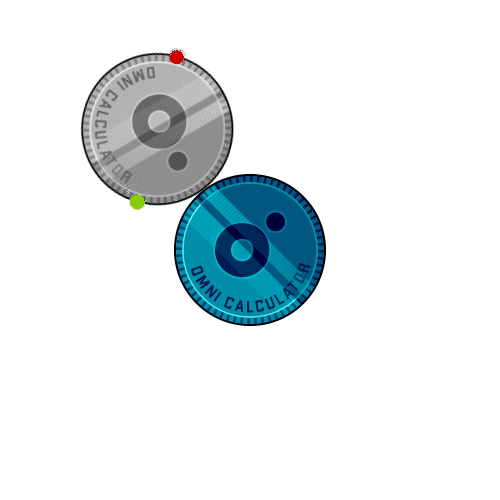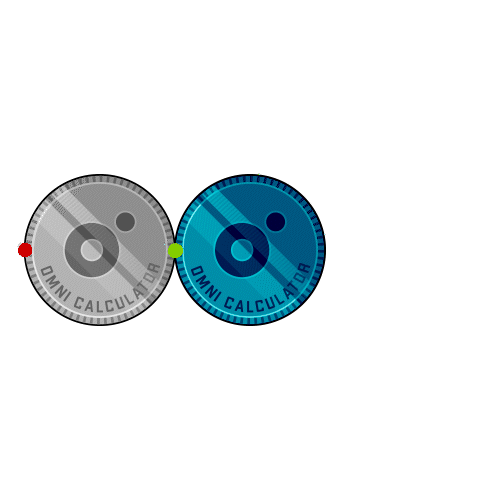
Think about it: if you walk in half a circle (and the circle is big enough like, for example, the Cerro Mastratigo roundabout in Spain, with a staggering 400 meters radius), you end up facing the opposite direction to the one you had at the start, even though you never perceived this rotation.
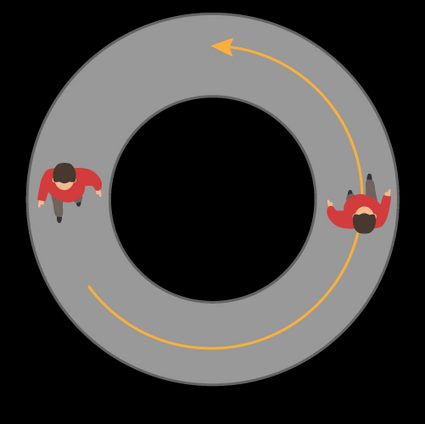
By completing the path around the other coin, the moving coin rotates another half-turn on its own, and the curvature of the path contributes to a last .
A few words on reference systems
As you look at the coin rotating, you belong to an "external" reference system. However, we can identify three views of the problem, each with a particular twist on the coin rotation paradox.
-
The stationary coin reference frame. Imagine standing on the stationary coin with a friend standing on the rotating one, looking forward. After their coins rotate for half of a circumference strung around you, they'd face backward, in the opposite direction from the one at the beginning: from your reference frame, the coin rotated as if it moved on a straight line.
-
The rotating coin reference frame. Imagine now being the friend in the story above. From their perspective, a person on the stationary coin rotated , a full rotation.
-
The point of contact reference frame. From this point of view, both coins rotate half a turn, ending with both upside-down.
All of these reference frames tell the truth from their perspective.
Earth and Moon: how to get rid of a rotation
What if we slide one of the coins or the other, ensuring the point of contact doesn't change? You would immediately know the outcome of this process: after half a turn, the coin would be upside-down, only to return to normality after a complete rotation.
How many times did the coin rotate? This time only once. Notice that it still rotated around its axis. However, it does this at the same time. It completes a revolution around the fixed coin: the exact mechanism is found in tidally-locked moons, like Earth's Moon: the result is that we only see one face of our natural satellite.
The mathematics of coin rotation: proof of the coin rotation paradox
In this section, we will give you a solid mathematical explanation of the coin rotation paradox. The proof of the coin rotation paradox starts with a generic case, where the same mechanism we analyzed is applied to two coins with generic radii and . Assuming , we will rotate the circle with radius while keeping the other stationary.
Start by placing the coins side-by-side and connecting the centers of the circles: mark the two horizontal radii on that line, and keep them as a reference. We can call the points and , generating the segments and . The two points are initially in contact. In the same position, we identify the tangent point , a moving point on the circumferences matching the point of contact between the coins, and a point on the rotating circumference, (which corresponds to the initial point of contact).

Start rotating the coin, as usual, without slipping, and stop after a short time. The setup now looks like in the image below.
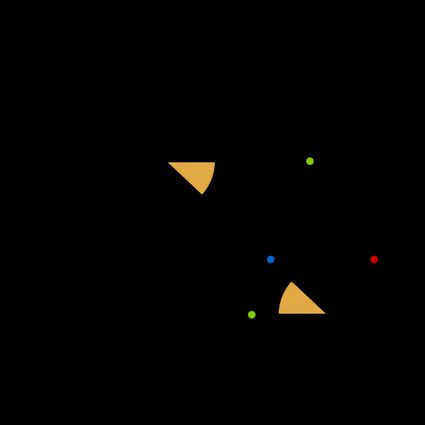
Notice how the segments and kept their orientation. We can identify two arcs on the rotating coin. One due to the rotation proper of the coin, , and one associated with the rotation around the fixed coin: . The two arcs sum to the larger arc .
Take the sum of these arcs: . Notice how you can find an analog on the fixed coin for : . Rewrite the sum:
By noticing how the segments and remain parallels, we can identify the angle and define the lengths of the arcs as a function of this parameter.
Rewrite this equation in a shorter way:
We notice, at this point, that a complete rotation of the rotating coin is given by:
Using the formula for calculating the circumference. Compare the two results:
Isolate , and rewrite:
is the angle centered in the fixed coin corresponding to a complete rotation of the rotating coin: we can equate these two angles thanks to the property of parallel lines (you can explore them at our parallel line calculator). To find the total number of rotations of the rotating coin, we multiply this angle by a number such that:
To find , we write:
From this equation, you can easily see the result of the original coin rotation paradox. Substitute :
How to use the coin rotation paradox calculator
We implemented a generalization of the coin rotation paradox. Insert the radii of the two coins, and let us compute the number of complete revolutions performed by the rotating coin after running along the complete circumference of the fixed one.
🙋 Are you interested in flipping coins rather than rotating them? Our coin flip probability calculator introduces probability and events easily!
FAQs
What is the coin rotation paradox?
The coin rotation paradox is an interesting example of how the shape of a path affects our perception of movement in space. In the coin rotation paradox, a coin rotates along the circumference of another coin of identical size.
If we stretched the path in a straight line, the coin would rotate once. However, as we close the path in a circumference, another rotation appears out of thin air. How did it happen? Bending the path introduced a curvature: the second rotation appears only because of our external reference frame.
How many times does a coin rotate around another coin?
If the two coins are identical in size, and slippage is not allowed, the rotating coin will complete two rotations by the time it reaches the starting point again. This seemingly unintuitive result stems from the fact that the path over which the coin is rotating is itself a circle, thus contributing an extra rotation. Rolling the coin on a linear path with an identical length would result in a single rotation.
How do I calculate the number of rotations of a coin around another coin?
To calculate the number of rotations of a coin around another fixed coin, if slippage is not allowed, follow these easy steps:
- Measure the diameter of the fixed coin, and divide it by 2 to find the radius rf.
- Find the radius of the rotating coin rr in the same fashion.
- Compute the ratio rf/rr.
- Add it to 1.
The final formula is:
N = 1 + rf/rr
How many rotations does a coin complete with slippage?
If the point of contact between two coins only moves along the circumference of the fixed coin, then, after a complete revolution around the fixed coin, the rotating one would have completed a single rotation. This is due to the slippage, as it causes one "face" of the rotating coin to always point toward the centers of the fixed one. This system resembles the Moon's movements around Earth — each revolution of our satellite corresponds to a single rotation.