Clock Angle Calculator

The clock angle calculator will help you solve some common clock math problems, such as, 'How to find the angle of clock hands given a time?'

Is it that time when you start learning about angles at school? Or maybe you enjoy solving math problems for fun and are unsure whether you have the correct answer? ⏰

Keep reading to find out:

• How much analog clock hands move with every hour and minute;
• How to find the angle between clock hands using only common sense;
• How to find the angle with clock angle formulas; and
• Why you should always visualize clock math problems.

Our brilliant clock angle calculator will help you with all your clock angle needs. So, let's get going! There's no time to spare.

Look at an analog clock. The shorter, hour hand makes a full turn in 12 hours. It means that each hour, it moves by 30 degrees.

360° / 12 = 30°

But the hour hand doesn't move once every hour! Each minute, it moves by half a degree.

30° / 60 = 0.5°

The minute hand rotates completely in 60 minutes. So, every minute it moves by 6 degrees.

360° / 60 = 6°

To find the angles created by clock hands, you can use two methods:

1. The first method is for those who prefer to come to the solution with logic and without any formulas.

2. The second method is for those who like using formulas.

As you know, computers don't have common sense, so our clock angle calculator works thanks to formulas. As you're probably not a computer, feel free to use the method you're more comfortable with.

Finding the angle between the hour hand and the minute hand is easy when there is a full hour on a clock. The minute hand targets the number 12, so the angle equals the hour multiplied by 30 degrees!

So, let's try that on an example:

Example 1. What is the angle between the hands of a clock at 4 o'clock?

Angle between clock hands = 30° × 4 = 120°

The angle you're looking for is 120 degrees. But did you know that there are two angles between the hands of an analog clock? The second one fills the space on the other sides of an hour and minute hands. You can find it by subtracting one angle from a full turn (360°):

360° − 120° = 240°

Our clock angle calculator will give you two angles extended clockwise:

• The angle from hour to minute hand, in this example – 240°; and
• The angle from minute to hour hand, here – 120°.

Now, let's see how to find the angle between clock hands without using any formulas on a harder clock math problem:

Example 2. The time on an analog clock reads 10:14. What's the angle between clock hands?

First, draw a clock, and mark characteristic parts of the angle.

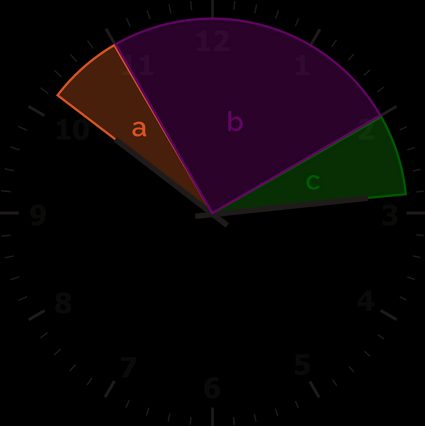
We started by marking the angle b because it's the easiest to find its size. It contains 3 whole hours (from number 11 to number 2), so it equals:

b = 3 × 30° = 90°

Then, we marked two remaining spaces with a (next to the hour hand) and c (next to the minute hand).

First, let's find a. We see from the image that it's smaller than 30°. The easiest way to find a is to see how far the hour hand is from the number 10. The angle between the hour hand and the number 10 on a clock is 14 minutes times 0.5°.

14 × 0.5° = 7°

So, how far is the hour hand from the number 11?

a = 30° − 14 × 0.5° = 30° − 7° = 23°

Lastly, we have to find the angle c. The minute hand moves between the number two to where it is now in four minutes. We already know that it also moves 6° every minute. So, c is equal to:

c = 4 × 6° = 24°

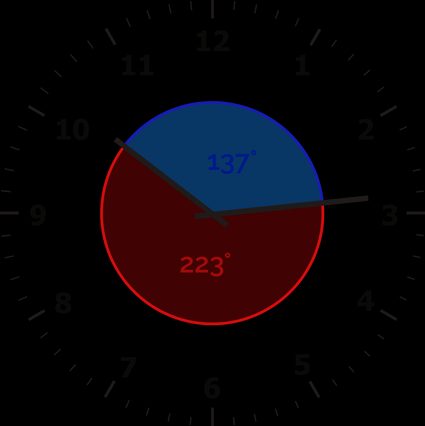
The angle between the hour hand and the minute hand equals:

Angle between clock hands = 90° + 23° + 24° = 137°

Remember – there are two clock angles! The other one is:

360° − 137° = 223°

How to find the angle of clock hands in a harder example

1. Again, start by drawing a clock.

2. Mark the angle between the minute hand and 12 o'clock. We already know that the minute hand moves by 6° each minute. So, to calculate the angle between the minute hand and 12 o'clock, multiply the number of minutes by 6 degrees.

   Angle_mins = 6° × number of minutes

3. Now, mark the angle between the hour hand and 12 o'clock. Remember that the hour hand moves with every minute. So, to find the correct angle, we also have to consider the number of minutes. So, the clock angle formula for the hour hand is:

   Angle_hrs = 30° × number of hours + 0.5° × number of minutes

   because the hour hand moves 30° with every full hour and then 0.5° every minute.

4. Lastly, find two clock angles. To find the first one, subtract the smaller angle from the bigger one. In other words, find the absolute value of the difference of two angles:

   First angle between clock hands = |Angle_hrs − Angle_mins|

• As in the previous method, the other angle is elementary (together, they make a full circle):

  Second angle between clock hands = 360° − First angle between clock hands

Let's use these instructions to solve a clock math problem:

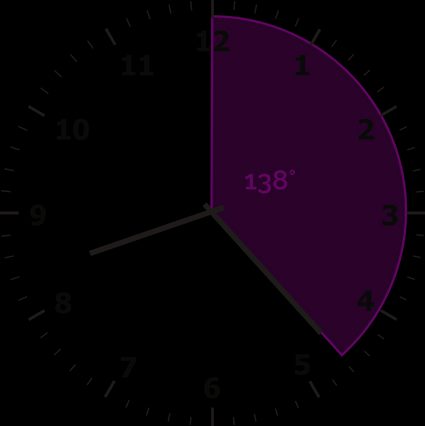
Example 3. Find the angle between the clock hands at 8:23.

• First, find the angle of the minute hand. Use the formula for the minute hand:

  Angle_mins = 6° × 23 = 138°

• Second, find the angle of the hour hand:

  Angle_hrs = 30° × 8 + 0.5° × 23 = 240° + 11.5° = 251.5°

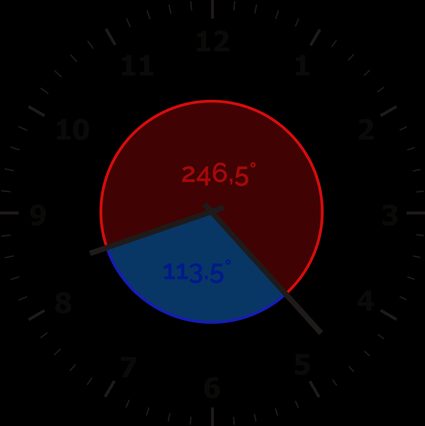
• Lastly, subtract the values:

  The angle of the hour hand is bigger than the angle of the minute hand, so:

  Angle_hrs − Angle_mins = 251.5° − 138° = 113.5°.

  The first angle between the clock hands is 113.5°.

• If needed, find the second angle:

  360° − First angle between clock hands = 360° − 113.5° = 246.5°

Now, choose your favorite method and solve all your clock math problems! And remember — you can always check your answer in our clock angle calculator! Before you go, in the angle conversion calculator, you can learn how to convert between different units for describing angles.