Angle Between Two Vectors Calculator

With this angle between two vectors calculator, you'll quickly learn how to find the angle between two vectors. It doesn't matter if your vectors are in 2D or 3D, nor if their representations are coordinates or initial and terminal points – our tool is a safe bet in every case. Play with the calculator and check the definitions and explanations below; if you're searching for the angle between two vectors formulas, you'll definitely find them there.

In this paragraph, you'll find the formulas for the angle between two vectors – and only the formulas. If you'd like to understand how we derive them, go directly into the next paragraph, How to find the angle between two vectors.

Angle between two 2D vectors

1. Vectors represented by coordinates (standard ordered set notation, component form):

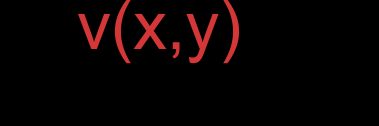
For vector $\boldsymbol a$:

And $\boldsymbol b$:

The angle is:

2. Vectors between a starting and terminal point:

For vector $\boldsymbol a$:

And:

So vector $\boldsymbol a$ is:

For vector $\boldsymbol b$:

And:

So vector $\boldsymbol b$ is:

And:

Angle between two 3D vectors

1. Vectors represented by coordinates:

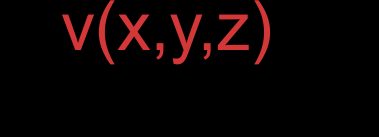
And:

Then:

2. Vectors between a starting and terminal point:

For vector $\boldsymbol{a}$:

And:

So:

For vector $\boldsymbol{b}$:

And:

So:

Find the final formula analogically to the 2D version:

Also, it is possible to have one vector defined by coordinates and the other defined by a starting and terminal point, but we won't let that obscure this section even further. All that matters is that our angle between two vectors calculator has all possible combinations available to you.

OK, the above paragraph was a bit of a TL;DR. As a way of better understanding the formulas for the angle between two vectors, let's check where they come from:

1. Start with the basic geometric formula to calculate the dot product:

   The dot product is defined as the product of the vectors' magnitudes multiplied by the cosine of the angle between them (here denoted by $\alpha$):

2. Then, make the angle the subject of the equation:

   Divide by the product of the vectors' magnitudes:

Find the inverse cosine of both sides:

3. Afterward, we need to brush up on the definition of a vectors' magnitude:

   As magnitude is the square root of the sum of the vector's components to the second power, we find out that:

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2}$ in 2D space; and

   • $|\boldsymbol{v}| =\sqrt{x^2+y^2+z^2}$ in 3D space.

Did you notice that it's the same formula as the one used in the distance calculator? And that it comes directly from geometry — learn how with the Pythagorean theorem calculator?

4. Use the algebraic formula for the dot product (the sum of products of the vectors' components), and substitute in the magnitudes:

In 2D space:

If vectors $\boldsymbol{a}$ and $\boldsymbol{b}$ are, respectively:

And:

In 3D space:

If vectors $\boldsymbol{a}$ and $\boldsymbol{b}$ are, respectively:

And:

Then:

And that's it!

Additionally, if your vectors are in a different form (you know their initial and terminal points), you'll need to perform some calculations beforehand. The aim is to reduce them into standard vector notation.

If your example vector is described by the initial point $A=(x_1, y_1)$ and the terminal point $B=(x_2, y_2)$, then vector$\boldsymbol{a}$ may be expressed as:

Still not making sense? No worries! We've prepared some exemplary calculations to make sure it's as clear as crystal.

Assume that we want to find the angle between two vectors:

and $\boldsymbol{b}$ defined as the vector between point $A = (1, 1, 2)$ and $B = (-4, -8, 6)$.

What do we need to do?

1. First, calculate vector $\boldsymbol{b}$, given the initial and terminal points:

2. Then, find the dot product of vectors $\boldsymbol{a}$ and $\boldsymbol{b}$:

3. Next, determine the magnitude of vectors:

And:

4. Finally, use the transformed dot product equation:

And there you go! You've just calculated the angle between two 3D vectors. Congratulations!

If you want to learn more coordinate geometry concepts, we recommend checking the average rate of change calculator.

So, how does our angle between two vectors calculator work? Follow these step-by-step instructions:

1. Choose your vector space. Let's consider the same example as in the previous paragraph. Our vectors and points have three coordinates, so we need to pick the 3D option.

2. Pick the first vector's representation. The first vector is in standard notation, so we leave the default value: coordinate representation.

3. Input the first vector. Type in $x = 3,$ $y = 6,$ and $z = 1$.

4. Choose the second vector's representation. This time we need to change it to point representation.

5. Enter the second vector's values. Input $\boldsymbol A = (1,1,2)$ and $\boldsymbol B = (-4,-8,6)$ into the proper fields.

6. The tool has found the angle between two 3D vectors the moment you fill out the last field. In our case, it's $150.2\degree$ – which is, of course, the same result we got from the manual calculations.

A vector is a geometric object that has both magnitude and direction. It's very common to use them to represent physical quantities such as force, velocity, and displacement, among others.

The angle formed between two vectors is defined using the inverse cosine of the dot products of the two vectors and the product of their magnitudes.

To calculate the angle between two vectors in a 2D space:

1. Find the dot product of the vectors.
2. Divide the dot product by the magnitude of the first vector.
3. Divide the resultant by the magnitude of the second vector.

Mathematically, angle α between two vectors [x_a, y_a] and [x_b, y_b] can be written as:

α = arccos[(x_a x_b + y_a y_b) / (√(x_a² + y_a²) × √(x_b² + y_b²))].

To calculate the angle between two vectors in a 3D space:

1. Find the dot product of the vectors.
2. Divide the dot product by the magnitude of the first vector.
3. Divide the resultant by the magnitude of the second vector.

Mathematically, angle α between two vectors [x_a, y_a, z_a] and [x_b, y_b, z_b] can be written as:

α = arccos[(x_a x_b + y_a y_b + z_a z_b) / (√(x_a² + y_a² + z_a²) × √(x_b² + y_b² + z_b²) )].