AAS Triangle Calculator

Use the AAS triangle calculator to calculate the area and the rest of the dimensions of an AAS triangle.

In the accompanying text of this tool, we discuss:

• The AAS triangle congruence;
• How to solve an AAS triangle;
• How to calculate the height for an AAS triangle; and
• How to obtain the AAS triangle formula for area.

Enjoy! 🔺

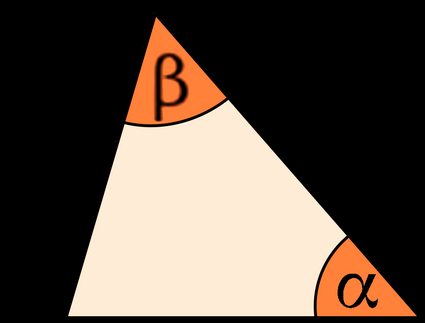
AAS stands for Angle-Angle-Side. An AAS triangle is a triangle in which one side $a$, the opposite $\alpha$, and adjacent $\beta$ angles are known.

In geometry, two figures or objects are said to be congruent if their shape and size are the same. Triangles classification in SAS, SSS, ASA, or AAS simplifies the study of triangle congruence.

In the case of AAS triangles, two triangles are congruent if two consecutive angles and the non-included side of one triangle are equivalent to the corresponding two angles and side of the second triangle. These are AAS congruent triangles.

If we have an AAS triangle and want to know the other three dimensions: $b$, $c$, and $\gamma$, we can resort to some good old never-out-of-style trigonometry.

Let's see how to calculate them:

Third angle $\gamma$

For this one, we need to remember that the internal angles of any triangle will always add $\pi$ or $180°$. With this in mind, simply subtract the two known values of the angles from $180°$ to find the missing angle:

Sides $b$ and $c$

For these two, we'll be using the law of sines:

We may start by finding the expression to calculate the base $b$, since the side $a$, angles $\alpha$, and $\beta$ are all known:

Similarly, given that we have an expression for the angle $\gamma$, we can use the following equation derived from the law of sines to determine the side $c$:

or

To find the AAS triangle's area, we'll be using the general triangle area formula:

In the case of our AAS triangle, the initial known dimensions are the side $a$ and angles $\alpha$ and $\beta$:

Notice from the area equation that we'll need to know the base $b$ and height $h$ to be able to calculate the area. In the previous section, we already mentioned how to calculate $b$ with the law of sines:

We need to figure out how to obtain the height $h$. By drawing the height of the triangle, our triangle will be divided into two right triangles:

• The triangle of hypotenuse $a$ and height $h$; and
• The triangle with hypotenuse $c$ and height $h$.

In this case, since we have the value for the side $a$, we'll use the first triangle. By employing the expression for the sine of the angle $\gamma$, we can clear the height $h$:

Even though $\gamma$ is not initially provided, we already saw that we can easily obtain its value by subtracting $\alpha$ and $\beta$ from $\pi$ — $\gamma = \pi - \alpha - \beta$.

All that's left is to replace all of these expressions in our original area formula:

To express the area only in terms of the initial knowns, we can use the properties of sines: $\text{sin}(\pi - \theta) = +\ \text{sin}(\theta)$. Therefore $\text{sin}(\gamma) = \text{sin}(\pi - \alpha- \beta) = +\ \text{sin}(\alpha + \beta)$. Then the AAS triangle area formula is:

Use the AAS triangle calculator to determine the area, third angle, and the two missing sides of this type of triangle. Let's have a look at how to use this tool:

1. In the first section of the calculator, enter the known values of the AAS triangle. These are the two consecutive angles β and α and the non-included side a.
2. In the section Results, the calculator will show you the results of the AAS triangle. Here you'll get the angle γ, other sides b and c, height h, and the Area of the triangle.
3. You are done! 😀

If you enjoyed using the AAS triangle calculator, you might be interested in some of our other triangle-related tools:

• Triangle area calculator;
• AAA triangle calculator;
• Midsegment of a triangle calculator;
• Acute triangle calculator;
• Circumcenter calculator;
• Triangle congruence calculator;
• Obtuse triangle calculator;
• Oblique triangle calculator;
• Base of a triangle calculator;
• SAS triangle calculator;
• SSS triangle calculator; and
• ASA triangle calculator.