Thread Calculator

This thread calculator will help you find the different nut and bolt thread dimensions under ISO metric standards. In this metric thread calculator, you will learn:

• How to determine metric thread sizes;
• How to read and understand metric thread callouts;
• The formulas for metric external thread dimensions;
• The formulas for metric internal thread dimensions; and
• What metric thread class means.

Let's start by learning what threads are. 🔩

Threads can mean a lot of things. In this thread calculator, we'll discuss the screw thread made out of grooves and ridges wrapped around a cylindrical or conical metal shaft in a helix pattern. The thread's helix spiral pattern acts like an inclined plane that translates rotational movement to axial movement while gaining some mechanical advantage.

As a result, a screw thread offers a locking feature that would require a good amount of shear stress to break, making it great for fastening objects together. This kind of thread can be an external thread (like on a screw or bolt) or an internal thread (like what we see inside a nut). We call these threaded materials threaded fasteners.

Though we can also see threads in other applications, like bottle caps, bulbs, pipes and connectors, and even worm gears, this thread calculator focuses specifically on metric threads. Metric threads have symmetrical V-shaped threads that form 60º-angle grooves and have basic dimensions shown below:

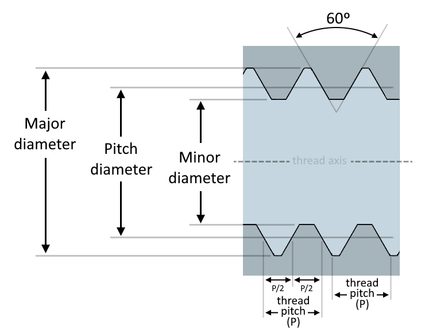
The major diameter is the largest diameter of an external or internal thread. We also call this diameter the gross diameter or nominal diameter of the thread. On the other hand, the minor diameter is the smallest diameter of an external or internal thread. We also call it the root or core diameter of the thread.

In between these two diameters is the pitch diameter. The pitch diameter is the thread's diameter in which the thickness of the thread and the space between two threads are equal. We can approximate the pitch diameter's value by taking the average of the minor and major diameters of the thread. Visit our pitch diameter calculator to learn more about it.

Thread pitch, or simply pitch is the distance between a point on one thread to the corresponding point on the thread adjacent to it (for example, the measurement from crest to crest or from root to root). Learn more about thread pitch by checking out our thread pitch calculator.

Understanding your metric threads starts with knowing how to read metric thread callouts. A thread callout is the same as a threaded fastener's label when you see them in a hardware store. Any thread standard has its own thread callout, and here is an example of a metric thread callout:

$\text{M10 × 1 × 25}$

We read this callout as "M-ten by one by twenty-five" where:

• $\text{M}$ stands for "metric" and means that the threaded fastener follows the ISO Metric Standard;
• $10$ in this case, which is the number affixed to the letter M, represents the basic major diameter of the thread;
• $1$ represents the thread pitch; and
• $25$ is the length of the shaft.

All the measurements in a metric thread callout are in millimeters.

Now that we can read metric thread callouts, we can start calculating our threads' different dimensions. Knowing how to determine metric thread sizes gives us another way to distinguish one threaded fastener from another. As a guide, we are going to use this illustration:

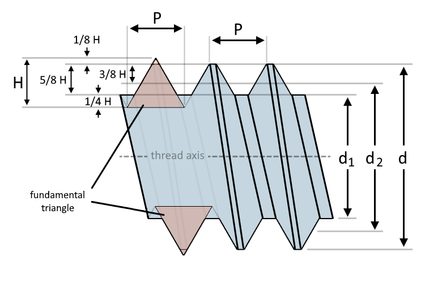
From the illustration above, we can see that we can use fractions of H to determine the different metric thread dimensions given the basic major diameter ($\small{d}$). But what is H? $\small{H}$ is the height of the thread's fundamental triangle. The fundamental triangle is the projected equilateral triangle we can form from the thread's cross-section. We can get its height measurement using this formula:

where:

• $P$ – Thread pitch.

By analyzing the same diagram above, we can then formulate the following equations to find the other basic diameters of an external thread:

• $d_1 = d - 2 \times \frac{5}{8} \times H$

• $d_2 = d - 2 \times \frac{3}{8} \times H$

where:

• $d$ – Basic major diameter;
• $H$ – Height of fundamental triangle;
• $d_1$ – Basic minor diameter; and
• $d_2$ – Basic pitch diameter.

As a rule of thumb, an internal thread of a given specified size should have the same basic diameters as an external thread of the same specified size. This means that $d_1 = D_1$, and $d_2 = D_2$ where $D_1$ and $D_2$ are the internal thread's basic minor diameter and basic pitch diameter, respectively.

From what we have already discussed, the basic diameters of a pair of external and internal threads precisely match each other. However, most of the time we provide some allowances to our threads to have some leeway when fitting them together. This is where metric thread classes come into play.

Metric thread classes indicate a metric thread's tolerance grade and tolerance position. Each tolerance grade and position have corresponding equations that will tell us how much deeper we should cut or cold-roll the threads to achieve those allowances we want.

However, there are limitations as to how much we could deviate from the basic thread dimensions. Therefore, it's good to know our thread's allowable maximum and minimum diameters.

Here are the formulas that we use to find those maximum and minimum diameters:

For external thread major diameter (d):

• $d_\text{max} = d + es$
• $d_\text{min} = d + es - T_\text{d}$

For external thread minor diameter (d₁):

• $d_\text{1max} = d_1 - es - 2 \times y$
• $d_\text{1min} = d_1 - es - 2 \times z$

For external thread pitch diameter (d₂):

• $d_\text{2max} = d_2 + es$
• $d_\text{2min} = d_2 + es - T_\text{d2}$

For internal thread major diameter (D):

• $D_\text{min} = D + EI$

For internal thread minor diameter (D₁):

• $D_\text{1min} = D_1 + EI$
• $D_\text{1max} = D_1 + EI + T_\text{D1}$

For internal thread pitch diameter (D₂):

• $D_\text{2min} = D_2 + EI$
• $D_\text{2max} = D_2 + EI + T_\text{D2}$

where:

• $es$ and $EI$ – Fundamental deviations, upper and lower deviations, respectively;
• $T$ – Tolerances for their corresponding diameters (i.e., $T_\text{d2}$ is the external thread pitch diameter ($d_2$) tolerance); and
• $y$ and $z$ – Adjustment values for maximum minor diameter and mininmum minor diameters, respectively.

Here are the equations we use to find the fundamental deviations depending on what tolerance position the threads need to be:

Fundamental deviations for external threads

• For e position: $\small{es = -(50 + 11 \times P) / 1000}$;
• For f position: $\small{es = -(30 + 11 \times P) / 1000}$;
• For g position: $\small{es = -(15 + 11 \times P) / 1000}$; and
• For h position: $\small{es = 0}$.

Fundamental deviations for internal threads

• For G position: $\small{EI = (15 + 11 \times P) / 1000}$; and
• For H position: $\small{EI = 0}$.

On the other hand, here are the different general equations that we use to determine the tolerances based on the tolerance grade of the thread:

For external threads

• $\small{T_\text{d}(n) = k \times (180 \times P^{2/3} - 3.15 \times P^{-1/2}) / 1000}$; and
• $\small{T_\text{d2}(n) = k \times (90 \times P^{0.4} \times d^{0.1}) / 1000}$

For internal threads

• $\small{T_\text{D1}(n) = k \times (433 \times P - 190 \times P^{1.22}) / 1000}$ (for 0.2 mm ≤ P ≤ 0.8 mm);
• $\small{T_\text{D1}(n) = k \times (230 \times P^{0.7}) / 1000}$ (for P ≥ 1.0 mm);
• $\small{T_\text{D2}(n) = k \times (90 \times P^{0.4} \times d^{0.1}) / 1000}$

In these equations, the value for $k$ depends on which tolerance grade the threads use, indicated by $n$. A bolt with a tolerance grade of $n = 6$ for its major diameter should use $k = 1.0$ when solving for $T_\text{D1}$. Here are the other values of k in the table below:

For the minor diameter, you can also see that we've got there two other adjustment variables, $y$ and $z$, incorporated in the equation. Below are the equations we use for that:

We calculate $R_\text{min}$ to be equal to $\frac{P}{8}$.

For threads with specified thread class details, we can add their codes at the end of the thread callout. For example, an external thread labeled as $\text{M30 × 2 × 40 - 5g6g}$ means that it has a pitch diameter tolerance grade of $5$ and a major diameter tolerance grade of $6$, both of which follow a $\text{g}$ tolerance position.

Usually, we only perform manual calculations to find a thread's basic diameters. As you may have found out, it would take many extra steps to determine the diameter limits. And that is where our metric thread dimensions calculator comes in very handy! Here are steps to follow in using our tool:

1. Choose which dimensions you want to calculate – metric external thread dimensions, internal thread dimensions, or both.
2. Select the thread pitch of your threads from the drop-down menu.
3. Input the basic major diameter of your threaded fastener. You can get this measurement from the thread callout or measure this dimension using a pair of precision calipers.
4. Finally, from the Tolerance class details section of our metric thread calculator, select your fastener's different tolerance grades and tolerance positions, whichever is known to you. You can also see this detail on your metric thread callout.

Once you've done the steps above, you'll immediately see not just the basic diameters but also the maximum and minimum diameters of your thread.

You can also click on the Advanced mode button below our metric thread calculator if you wish to explore the different preliminary measurements used in the calculations, such as the height of the fundamental triangle, deviations, tolerance values, and adjustments.

Let's say we have a bolt with a basic major diameter (d) of 10 mm and a thread pitch (P) of 1.5 mm. To find its pitch diameter:

1. First, calculate the height of its fundamental triangle (H) using H = P × (√3) / 2. H = 1.5 mm × (√3) / 2 = 1.299 mm.
2. Then, obtain for the pitch diameter (d₂) using d₂ = d - 2 × (3 / 8) × H, d₂ = 10 mm - 2 × (3 / 8) × 1.299 mm = 9.026 mm.

Let's say we have a bolt with a basic major diameter (d) of 20 mm and a thread pitch (P) of 2 mm. To find its minor diameter:

1. Calculate the height of its fundamental triangle (H) using H = P × (√3) / 2. H = 2 mm × (√3) / 2 = 1.732 mm.
2. Obtain for the minor diameter (d₁) using d₂ = d - 2 × (5 / 8) × H, d₂ = 20 mm - 2 × (5 / 8) × 1.732 mm = 17.835 mm.

An M6 thread has a basic major diameter of 6 mm. Typically, metric thread callouts also come with the thread pitch, such that an M6 × 1 threaded bolt has a basic major diameter of 6 mm and a thread pitch of 1 mm. When purchasing a threaded fastener, make sure you have both the diameter and the thread pitch. Without one of those measurements, you could buy the wrong-sized hardware.

The nominal diameter of a thread is the diameter for which a thread is known. We use the nominal diameter for the general identification of threads. For example, a thread with a callout of M10 × 1.5 has a nominal diameter of 10 mm. Generally, the nominal diameter of a thread is the same as the basic major diameter of the thread.