Diffusion Coefficient Calculator

Q: What is the diffusion coefficient?

The diffusion coefficient is a parameter characteristic of particles in solution that describes the easiness with which they move from regions with higher concentration to regions with lower concentration due to random motion ( Brownian motion ). The diffusion coefficient depends on the solvent's temperature and viscosity and the shape and size of the solute's particles.

Q: How do I calculate the diffusion coefficient?

To calculate the diffusion coefficient in Einstein's relation , follow these simple steps: Identify the shape and size of the particles of the solute. Compute the friction coefficient of the particles in the solvent. This quantity depends on the dynamic viscosity of the solvent. Multiply Boltzmann's constant by the absolute temperature of the solution . Divide the result by the friction coefficient. Remember to keep the units coherent. You are done!

Q: What is the diffusion coefficient of a spherical particle with r = 2 nm in water at 25 °C?

The diffusion coefficient is 1.2269 × 10 -10 m 2 /s . To find this result: Calculate the friction coefficient of the particle: ξ = 6π · η · r . ξ = 6π · 0.00089 Pa · s · 2 × 10 -9 m = 3.355 × 10 -11 s/kg . Multiply Boltzmann's constant and the absolute temperature of water : k B · T = 4.12 × 10 -21 J . Divide by the friction coefficient to find the diffusion coefficient: D = 4.12 × 10 -21 J/3.355 × 10 -11 s/kg = 1.2269 × 10 -10 m 2 /s .

Q: Why does the friction coefficient matter in the diffusion coefficient formula?

The friction coefficient is a measure of the easiness with which a particle of solute moves in the solvent . It depends mainly on three quantities: The solvent's viscosity ; The particle's shape ; and The particle's size . The lower the viscosity, the lower the friction coefficient. The size acts similarly, favoring small particles. In the formula for the diffusion coefficient, the friction coefficient balances the action of temperature on the magnitude of diffusion, hindering the random motion of particles.

Created by Davide Borchia

Reviewed by Purnima Singh, PhD and Adena Benn

Last updated: May 26, 2024

Table of contents:

With our diffusion coefficient calculator, you will learn how to find the diffusion coefficient starting from the friction coefficient for many shapes. Keep reading this article to learn:

What the diffusion coefficient is;
How to calculate the diffusion coefficient: formula derivation and the physics of the problem;
Variations of the formula for the diffusion coefficient;
Examples of calculations of the diffusion coefficient; and
Much more!

What is diffusion?

Diffusion is the motion of particles of any kind and suitable size in a medium according to the gradient of the concentration of said particles in a solvent. Diffusion is a type of mass transport which relies on random motions of the particles to gradually distribute mass according to the conditions of the considered system.

Diffusion is a well-studied phenomenon. Fick's laws describe the evolution of the particles' flux, either as a function of the concentration gradient or of time. We will start from the first Fick's law to learn how to calculate the diffusion coefficient. Let's go!

How to calculate the diffusion coefficient with Einstein relation

The formula for the diffusion coefficient, which we introduce in this calculator, is credited to Einstein and Smoluchowski. The two physicists derived the formula independently in situations where the diffusion of particles in a solution happens in the presence of an external force. In this case, Fick's first law takes the form:

J = -D\left(\frac{\mathrm{d}c}{\mathrm{d}x}\right) + \frac{c\cdot f}{\xi}

where:

$J$ — Concentration flow or current;
$D$ — Diffusion coefficient;
$c$ — concentration of the particles;
$f$ — External force; and
$\xi$ — Friction coefficient.

🙋 If you need to refresh your physics regarding friction, visit our friction coefficient calculator and our friction calculator!

In this formula, we can identify two contributions: one from diffusion (the space derivative of the concentration) and the other from the external force. In the case of the Einstein-Smoluchowski relation, we assume that the flow is zero. This allows us to equate the two contributions in the following way:

D\left(\frac{\mathrm{d}c}{\mathrm{d}x}\right)=\frac{c\cdot f}{\xi}

We can rearrange the equation to isolate the concentration, even though mathematicians may get angry:

D\cdot\left(\frac{\mathrm{d}c}{c}\right) = \frac{f\cdot\mathrm{d}x}{\xi}

The solution to this equation is given by integration:

\ln\left(\frac{c(x)}{c(0)}\right)=\frac{-w}{D\cdot\xi}

where we introduced the natural logarithm and the quantity $w = \int f\mathrm{d}x$ . Exponentiate this quantity to isolate the concentration:

\frac{c(x)}{c(0)}=\mathrm{e}^{-\frac{w}{D\cdot \xi}}

We can equate this quantity to the famous Boltzmann distribution law, thus obtaining:

\mathrm{e}^{-\frac{w}{D\cdot \xi}} = \mathrm{e}^{-\frac{w}{k_\mathrm{B}\cdot T}}

This leaves us with the formula for the diffusion coefficient:

D = \frac{k_\mathrm{B}\cdot T}{\xi}

The diffusion coefficient formula

Let's take a deeper look at the formula for the diffusion coefficient:

D = \frac{k_\mathrm{B}\cdot T}{\xi}

In this expression, we can find:

$k_\mathrm{B}$ — Boltzmann's constant with value $k_\mathrm{B} = 1.380649\times10^{-23}\ \mathrm{J/K}$ ;
$T$ — Absolute temperature in kelvin; and
$\xi$ — Friction coefficient with units $\mathrm{s/kg}$ .

A quick glance at this formula suggests that:

The higher the temperature, the higher the diffusion coefficient; hence at higher temperatures, this method of mass transport is faster than at colder ones.
The higher the friction coefficient, the lower the coefficient. Particles with complex shapes tend to diffuse with more difficulties than streamlined ones.

The diffusion coefficient has units $\mathrm{m^2/s}$ .

The friction coefficient in the equation for the diffusion coefficient

The friction coefficient depends on both the size and shape of a particle. In the following table, you can find the expression for the friction coefficient for a few selected shapes. In the table, $\eta$ is the viscosity of the solvent, and $a$ and $b$ are the geometric sizes of the particle.

	Shape	Friction coefficient ( $\xi$ )
	Sphere (low $Re$ )	$6\pi\cdot \eta\cdot a$
	Disk (face on)	$16\cdot\eta\cdot a$
	Disk (edge on)	$(32/3)\cdot \eta\cdot a$
	Disk (random motion)	$12\cdot \eta\cdot a$
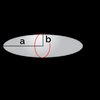	Ellipsoid (lenghtways)	$\frac{4\pi\cdot \eta\cdot a}{\ln(2\cdot a/b)+1/2}$
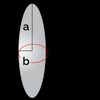	Ellipsoid (sideways)	$\frac{8\pi\cdot \eta\cdot a}{\ln(2\cdot a/b)+1/2}$
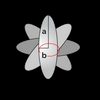	Ellipsoid (random motion)	$\frac{6\pi\cdot \eta\cdot a}{\ln(2\cdot a/b)}$

The first case, a sphere moving in fluids with a low Reynolds number (we talked about it at the Reynolds number calculator), is worth an honorable mention, as when it is substituted in the formula for the diffusion coefficient, it gives us the Einstein-Stokes relation:

D = \frac{k_\mathrm{B}\cdot T}{6\pi\cdot \eta\cdot a}

You can easily see the similarities with Stokes' law.

🙋 Our water viscosity calculator gives you the dynamic and static viscosity values for water at any temperature you need!

An example of the calculations of the diffusion coefficient

Let's take the... Sulfolobus ellipsoid virus 1, a rather mysterious virus discovered a few years ago in Costa Rica's hot springs. This virus has a peculiar ellipsoidal shape with dimensions $a = 115\ \mathrm{nm}$ and $b = 78\ \mathrm{nm}$ . Assuming that our little friend is tumbling randomly in its hot spring at a temperature of $90\ \degree\mathrm{C}$ , what is its diffusion coefficient?

We can use the diffusion coefficient formula for a randomly moving ellipsoid. Let's first compute the friction coefficient:

\begin{split} \xi&= \frac{6\pi\cdot \eta\cdot a}{\ln(2\cdot a/b)}\\[1.5em] &\!\!\!\! = \frac{6\pi\!\cdot\! 0.0003149\ \mathrm{Pa\!\cdot\! s}\cdot 115\ \mathrm{nm}}{\ln(2\cdot 112\ \mathrm{nm}/78\ \mathrm{nm})}\\[1.5em] &\!\!\!\!=6.312\times 10^{-10}\ \mathrm{s/kg} \end{split}

Next stop: the diffusion coefficient formula!

\begin{split} D& = \frac{k_\mathrm{B}\cdot T}{\xi}\\[1.5em] &=\frac{ 1.380649\times10^{-23}\ \mathrm{J/K}}{6.312\times 10^{-10}\ \mathrm{s/kg}}\\[1.5em] & \cdot (273.15+90)\ \mathrm{K}\\[1.5em] &=7.943\times10^{-12}\ \mathrm{m^2/s} \end{split}

A reasonable value!

How to use our diffusion coefficient calculator

Our diffusion coefficient calculator implements all the formulas we've seen for the friction coefficients of various shapes. Select the one that interests you and input the requested data.

Once you fill in enough fields, it will calculate the diffusion coefficient! Remember that you can use our tools in reverse, too: you can compute the friction coefficient starting from a measured diffusion coefficient value. This is a standard laboratory procedure to assess this quantity. The diffusion coefficient is relatively easy to measure compared to the friction coefficient of molecule-sized particles!

FAQ

What is the diffusion coefficient?

The diffusion coefficient is a parameter characteristic of particles in solution that describes the easiness with which they move from regions with higher concentration to regions with lower concentration due to random motion (Brownian motion). The diffusion coefficient depends on the solvent's temperature and viscosity and the shape and size of the solute's particles.

How do I calculate the diffusion coefficient?

To calculate the diffusion coefficient in Einstein's relation, follow these simple steps:

Identify the shape and size of the particles of the solute.
Compute the friction coefficient of the particles in the solvent. This quantity depends on the dynamic viscosity of the solvent.
Multiply Boltzmann's constant by the absolute temperature of the solution.
Divide the result by the friction coefficient. Remember to keep the units coherent.

You are done!

What is the diffusion coefficient of a spherical particle with r = 2 nm in water at 25 °C?

The diffusion coefficient is 1.2269 × 10^-10 m²/s. To find this result:

Calculate the friction coefficient of the particle:

ξ = 6π · η · r.

ξ = 6π · 0.00089 Pa · s · 2 × 10^-9 m = 3.355 × 10^-11 s/kg.
Multiply Boltzmann's constant and the absolute temperature of water:

k_B · T = 4.12 × 10^-21 J.
Divide by the friction coefficient to find the diffusion coefficient:

D = 4.12 × 10^-21 J/3.355 × 10^-11 s/kg = 1.2269 × 10^-10 m²/s.

Why does the friction coefficient matter in the diffusion coefficient formula?

The friction coefficient is a measure of the easiness with which a particle of solute moves in the solvent. It depends mainly on three quantities:

The solvent's viscosity;
The particle's shape; and
The particle's size.

The lower the viscosity, the lower the friction coefficient. The size acts similarly, favoring small particles.

In the formula for the diffusion coefficient, the friction coefficient balances the action of temperature on the magnitude of diffusion, hindering the random motion of particles.

Davide Borchia

Shape

Absolute temperature (T)

Radius (a)

Solvent viscosity (η)

Diffusion coefficient (D)

m²/s

Graham's law of diffusionHalf lifeLangmuir isotherm… 5 more