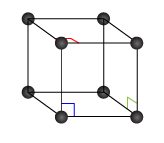
Cubic Cell Calculator

The cubic cell calculator will introduce you to the world of crystals: learn the mathematics underlying the most regular structure in nature, and find examples where you would never imagine!

Here you will learn:

• Some basics concepts of crystallography;
• The crystal structures in two and three dimensions;
• The types of cubic unit cells and the related lattices; and
• The calculations of the lattice parameter for the cubic lattices.

And much more. This article will make this topic... crystal clear! If you want to dig deeper in crystallography, check out our Miller indices calculator and our Bragg's law calculator too!

Crystallography deals with the arrangement of atoms in the ordered structures of crystalline substances.

Crystals are all around us, but more often than not, we dismiss them, not even noticing their tidiness and marvelous order. Go in your kitchen: the coarse salt and the metal of your pan are examples of crystalline materials.

The number of atomic species in a crystal defines the basis of the crystal itself. The basis is the first element required to describe a crystal.

Take a crystalline substance, and start breaking it. Piece after piece, you would be able to separate the sample until a final break would give you something that is not the crystal anymore: you just found the unit cell of that substance, the smallest possible element with all the properties of the crystal.

Unit cells are tightly packed: there can't be any empty spaces between them. This highly restricts their possible shapes.

There's one last concept we need to introduce: the Bravais lattice. The lattice is an array of vectors that describes the positions of the elements in a crystalline structure. The lattice is the second (and last) element used to describe a crystalline structure: you could say that crystalline structure = basis + lattice. You can find more about lattices at our lattice energy calculator.

For a two-dimensional crystalline structure, only the following shapes pack tightly:

• Parallelogram;
• Rhombus;
• Square;
• Rectangle; and
• Centered rectangle.

From there, we can identify the corresponding crystal families, the groups to which we can assign crystalline structure according to non-translational (rotation, inversion, and roto-inversion) transformations and translational transformations:

• Monoclinic for the parallelogram unit cell;
• Hexagonal for the rhomboidal unit cell;
• Tetragonal for the square unit cell; and
• Orthorhombic for both rectangular unit cells.

Increasing the dimensions to three gives us a slightly more complex picture: even if all of the unit cells were parallelepipeds, we can identify six crystal families:

• Triclinic;
• Monoclinic;
• Orthorhombic;
• Tetragonal;
• Hexagonal; and
• Cubic.

Different geometric transformations return a possible set of 14 Bravais lattices among these six families. We will analyze in detail the ones related to the cubic crystal family.

A cubic unit cell generates three Bravais lattices:

• The simple cubic lattice;
• The body centered cubic (BCC) lattice; and
• The face centered cubic (FCC) lattice.

Let's analyze them in detail!

The simple cubic lattice

In the simple cubic lattice, each atom sits at a corner of a cube. In a single cell, each corner contains an eighth of each atom. Since there are eight corners, the total "amount" of atoms in the simple cubic cell is one (the cell is a proper unit cell).

The body centered cubic lattice

Trace all the diagonals connecting maximally separated pairs of atoms in a simple cubic cell, and place an atom at their intersection: that's how you obtain a body centered cubic lattice. The addition of the atom in the center brings the total contained by the cell to $2$.

The face centered cubic lattice

On each face of the cube, trace the two diagonals and add an atom at their intersection. This would add $6$ halves of atoms, bringing the total to $3$.

The geometry of a unit cell is determined by a set of numerical values called lattice parameters or lattice constants.

The maximum number of lattice parameters is $6$: three angles and three spatial directions. However, symmetries reduce that number in many instances. For a cubic cell, in fact, the angles are already defined, all equal to $90\degree$. Similarly, the three spatial lattice parameters are equal to each other: this leaves us with a single lattice constant, $a$.

We can define the lattice constant with a simple mathematical formula for each of the three types of cubic lattices.

The only variable in the lattice parameter determination is the atomic radius of the species composing the crystal, $r$. We will first show the calculations for monoatomic crystals.

The lattice constant of a simple cubic crystal is:

Considering the cell is tightly packed with atoms, the minimum length of the side of the cube would be twice the radius.

What if we place an atom in the middle of the cell? The lattice constant of a BCC cell reflects its presence:

This result comes from the formula for the diagonal of a cube, $d=\sqrt{3}\times l$. Pack the cube tightly with an atom in the center, and you'll find that the diagonal has length equal to four times the atomic radius.

The last possible lattice is the face centered cubic one. To find the lattice parameter of such crystal, follow a reasoning similar to the one we applied to the BCC lattice.

Pack each face of the cube tightly with atoms. On each diagonal ($\sqrt{2}\times l$ long), you can fit again four atomic radiuses. This gives us:

Let's sum up the results:

• Lattice constant of a simple cubic cell: $a = 2\times r$
• Lattice constant of a BCC cell: $a = 4\times \frac{r}{\sqrt{3}}$
• Lattice constant of an FCC cell: $a = 4\times \frac{r}{\sqrt{2}}$

Calculating the lattice constant for diatomic crystals (where the basis is $2$) is a different matter. The values are usually computed experimentally using techniques like X-rays diffraction.

Our cubic cell calculator will give you the value of the lattice constant in a few quick steps.

First, input in the cubic cell calculator the value of the atomic radius of the atoms making up the crystal. You can find those values in tables like the one on this page.

Then, choose the type of cubic cell of interest, and we will return the value of the lattice parameter!

Take as example aluminum. Its atomic radius is $r= 1.43\ \text{\AA}$, and it crystallizes in a face centered cubic lattice. Its lattice parameter would be:

Probably around half of your kitchenware is made of aluminum — you can find a perfect face centered cubic crystal right in your kitchen! While you're there, check if you have a cast iron pan. Cast iron is an alloy of iron and carbon. Carbon lies in the defects of a body centered cubic iron crystal. What is the lattice constant of the body centered cubic iron? The atomic radius of iron is $r= 1.24\ \text{\AA}$.

A cubic call can be of three types:

• Simple cubic, with one atom in each corner;
• Face centered cubic, with an additional atom at the center of each face; and
• Body centered cubic, where a single atom is added in the center of the cell.

Only the second structure maximizes the occupation of space in the cell.

The lattice parameters are quantities that indicate the shape of a crystalline cell. There are six lattices parameters, three dimensions, and three angles. Their number can be smaller in the case of symmetries in the unit cell — for example, there is only one spatial lattice parameter in a cubic cell, a.

There are three formulas to calculate a cubic cell constant parameter a, depending on the type of cell itself,

• For a simple cubic cell: a = 2 × r;
• For a body centered cubic cell: a = 4 × r / √3; and
• For a face centered cubic cell: a = 4 × r / √2.

Here, r is the value of the radius.

Polonium has a lattice constant of 3.369 Å. The radioactive element is the only known atomic species that packs in the relatively unstable simple cubic structure. The value of the lattice parameter comes from the equation:

a = 2 × r = 2 × 1.67 Å = 3.369 Å

Where:

• a is the lattice constant; and
• r is the atomic radius.