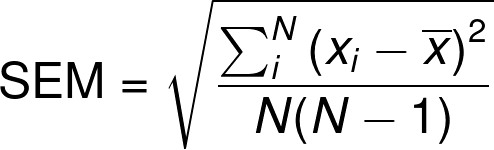Standard Error Calculator

Welcome to the standard error calculator, also known as the standard error of the mean (SEM) calculator. This is a great tool that helps you estimate the standard error of the mean of any dataset in the blink of an eye.

If you've studied statistics at all, you've probably already heard of the mean, median, and mode, but do you know how to calculate the standard error? If not – this is the right place to begin!

In the article below, you can also find the equation of the standard error of the mean, as well as a comparison of standard error vs. standard deviation. There is no time to waste, let's go!

To learn how to find a standard error, we first need to ask ourselves standard error of what?

In statistics, we can estimate the standard error of any parameter – a mean, a proportion, a difference of means, and many many more. Typically, if someone wants to know how to calculate the standard error, it's the standard error of the mean or SEM for short.

Great! So then, why do we want to know how to find the standard error?

Let's say we have a task to find the average height of adults within a country. Such measures usually form a normal distribution for large populations.

Ideally, we should measure everybody one by one, and eventually, we would get a precise, well-defined number. In practice, however, it's impossible from a time, money, and technical point of view, so we need to estimate such a value.

One approach is to take a relatively small group of people (a sample) and find their average height. It's almost certain that it won't be precisely the same as the one for the whole country. Still, we should be able to say that there is a high probability that the real result is within a range of values that we evaluated using the standard error. That's an example of a situation where this SEM calculator comes in handy!

The equation of the standard error of the mean in its most compact form is:

where:

• $x_i$ is the i^th measure;
• $\overline{x}$ (x-bar) stands for the mean value of our dataset; and
• $N$ is the number of data points.

To get familiar with the standard error formula, it's a good practice to follow these steps:

1. Evaluate the mean value ($\overline{x}$). It's usually the arithmetic average.

2. Find the differences $x_i - \overline{x}$ for every point.

3. Square the differences for each of the points separately, $(x_i - \overline{x})^2$.

4. Add up all of the squared differences $\sum(x_i - \overline{x})^2$.

5. Divide the sum by the product $N(N - 1)$.

6. Finally, work out the square root of this ratio.

As you can see, estimating the standard error of the mean for multiple points by hand can be really time-consuming. In such cases, using our standard error calculator is always a good idea, and you'll also avoid any mistakes!

In statistics, the standard deviation tells us about the variability of the respective measures from the mean. So what is the difference between standard deviation and standard error, then?

Simply speaking, the standard deviation is a parameter of a population (or a sample), while the standard error is an estimation of a particular value. In general, we can compute the standard error of any statistical value, but in most cases, we want to find the standard error of the mean.

To compare standard error vs. standard deviation, let's take a look at their formulas:

• $\text{standard deviation} = \sqrt{\sigma^2} = \sigma = \frac{\sum(x_i - \mu)^2}{N}$ for a population, where $\sigma^2$ is the variance of the set; or

• $\text{standard deviation} = \sqrt{s^2} = s = \frac{\sum(x_i - \overline{x})^2}{N-1}$ for a sample, where $s^2$ is the estimate of the variance.

• $\text{standard error of the mean} = \frac{s}{\sqrt{N}} = \frac{\sum(x_i - \overline{x})^2}{N(N-1)}.$

$\mu$ and $\overline{x}$ stand for the mean and sample mean, respectively.

In other words, we can say that SEM tries to estimate the mean value of the whole population within a certain margin of error.

Take a look at an example:

We want to estimate the average height of students in a school (a population). We take a group of 12 random pupils (a sample) whose heights (in cm) are 177, 182, 175, 194, 181, 177, 169, 180, 182, 186, 179, and 172.

The average height of this sample is x̄ = 179.5. Using our SEM calculator, you can find that the standard error of the mean equals SEM = 1.88. It tells us that the (real) mean height of students in this school is most likely between 177.62 and 181.38 (which is 179.5 ± 1.88).

At the same time, this sample's standard deviation is s = 6.52. This means that we can expect that the majority of students' heights (roughly 70%) to lie within the range [172.98, 186.02] (that is 179.5 ± 6.52).

Let's say we have a set of ten different values related to the weight of balls taken randomly from a production line. The numbers are: [5.5, 5.8, 6.1, 5.4, 5.5, 5.4, 5.9, 5.6, 5.9, 5.5]. The question is: what is the standard error of the mean for these measures? Let's do it step by step:

1. Work out the mean value of this set. x̄ = (5.5+5.8+6.1+5.4+5.5+5.4+5.9+5.6+5.9+5.5) / 10 = 56.6/10 = 5.66.

2. Calculate the difference between every number and the mean (xᵢ - x̄): [-0.16, 0.14, 0.44, -0.26, -0.16, -0.26, 0.24, -0.6, 0.24, -0.16].

3. Square them: [0.0256, 0.0196, 0.1936, 0.0676, 0.0256, 0.0676, 0.0576, 0.0036, 0.0576, 0.0256].

4. Sum them up: 0.0256 + 0.0196 + 0.1936 + 0.0676 + 0.0256 + 0.0676 + 0.0576 + 0.0036 + 0.0576 + 0.0256 = 0.544.

5. Make a fraction from this value and 90 (that is N(N-1)=10×9): 0.544 / 90 = 0.0060.

6. Compute the square root of the latter, resulting in the standard error of the mean: SEM = √0.0060 = 0.078.

7. We can also write that our estimated mean in the form x̄ = 5.660 ± 0.078, taking two significant figures into account.

You can always check the result with our standard error calculator!

By the way, have you heard about the skewness or mean absolute deviation? These are other parameters you can find while working with statistical data. Each of them carries additional information about your numbers!