Joint Probability Calculator
With our joint probability calculator, we aim to help you calculate the probability of multiple events occurring simultaneously. To explore related tools, check out our AND probability calculator and Bayes theorem calculator.
We've designed this tool to enhance your understanding of:
- What joint probability is;
- How to calculate joint probability; and
- The application of joint probability.
We have also included practical examples to help you comprehend the process of calculation using the joint probability formula.
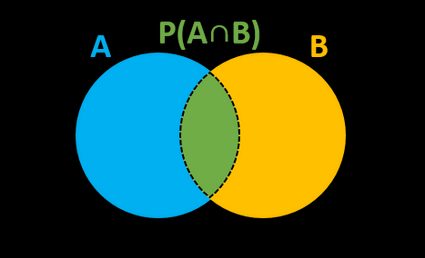
What is joint probability?
Joint probability is the likelihood of two or more events occurring at the same time. It's a core concept in probability theory and is essential for understanding how different events interact within a given context. Instead of analyzing each event in isolation, joint probability examines the relationship between events and how they occur together.
Joint probability is particularly useful in situations where outcomes are interconnected or where we want to understand the likelihood of specific combinations of events. For instance, events often influence one another, such as the probability of rain and the likelihood of someone carrying an umbrella. Joint probability allows us to analyze these connections and determine the possibility of such combined occurrences.
How to calculate joint probability — Joint probability formula
Now that we understand what joint probability is, let's explore an example to understand better how to calculate it.
Let's assume the following:
- Event A: Probability of a student passing a math exam =
P(A). - Event B: Probability of the same student passing a science exam =
P(B).
-
Determine if the events are independent or dependent.
The first step is to identify whether the events are independent or dependent.
- If the occurrence of one event doesn't affect the likelihood of the other, the events are considered independent;
- If the outcome of one event influences the probability of the other, the events are said to be independent dependent.
We will look at both here.
-
Input the probabilities.
The next step is to input the required probabilities.
Let's say the events are independent, you will need
P(A), which is the probability of passing math, andP(B), which is the probability of passing science. In this instance,P(A) = 0.8 (80%)andP(B) = 0.6 (60%).If the events are dependent, you will need
P(A)andP(B|A), which is the probability of passing science given that the math test is passed. For our example,P(A) = 0.8andP(B) = 0.7 (70%).You can use our probability calculator to facilitate the process.
-
Calculate the joint probability.
Once the probabilities are known, we can calculate the joint probability.
For the independent case, you can calculate the joint probability,
P(A and B), using the following formula:P(A and B) = P(A) × P(B)Thus, the joint probability is
0.8 × 0.6 = 0.48.When the events are dependent, you can calculate the joint probability using the formula below.
P(A and B) = P(A) × P(A|B)Hence, the joint probability is
0.8 × 0.7 = 0.56 (56%).
The application of joint probability
Joint probability is widely used across various fields to analyze relationships between events and make informed decisions. Some key applications include:
-
In statistics and data science, it's used in predictive modelling and hypothesis testing to understand correlations between variables. It's also used in machine learning to form probabilistic models like Bayesian networks and hidden Markov models.
-
In finance and risk analysis, joint probability helps assess the likelihood of market events occurring together, such as stock price movements or credit defaults.
-
Joint probability is also used to study the probability of diseases co-occurring or the effectiveness of treatments.
FAQs
What is the difference between independent and dependent events?
Independent events do not affect each other’s outcomes, while dependent events influence each other’s likelihoods.
Can joint probability be greater than 1?
No, probabilities, including joint probabilities, always range between 0 and 1. Anything below 0 or above 1 is considered wrong, as such probabilities do not exist.
What is the joint probability of 2 dependent events both with 50% probability?
The joint probability will be 25% or 0.25. You can calculate this by multiplying both probabilities with each other.
How can I calculate the joint probability of 2 dependent events?
You can calculate the joint probability in three steps:
-
Determine the probability of the first event.
-
Compute the probability of the second event.
-
Apply the joint probability formula:
joint probability = first probability × second probability