Torsion Spring Calculator
Use our torsion spring calculator to discover everything about these springy devices. Keep reading our article to learn:
- What is a torsion spring?
- What are the quantities defining a torsion spring?
- How do I calculate the stress of a torsion spring?
- The formulas to calculate a torsion spring's force.
And much more!
You will find our tool of great utility whenever torsional springs appear in your studies or work!
What is a torsion spring?
A torsion spring is a helpful mechanical device capable of storing and releasing rotational energy, usually delivering a defined amount of torque. Torsion springs are everywhere, from mundane applications like clothespins and safety pins.
As the name suggests, such devices work thanks to torsion, a rotation. We can define two types of torsion springs, distinguishing them by the place where the torsion happens in the element the spring is made of:
- If the torsion is applied at the axis of a helical-shaped spring created by twisting our element, we are dealing with a helical torsion spring.
- If the torsion is applied on the axis of the element itself, we have a torsion bar.
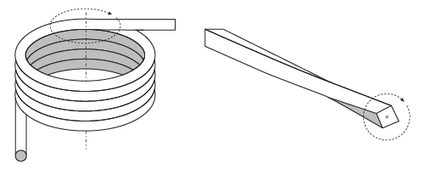
While the former's properties only depend on the material, we can carefully tune the latter's characteristics. Of course, the material with which we fabricate our spring matters, but the shape we are twisting it into is even of greater importance.
A helical torsion spring is a wire (usually round in section) coiled in a cylindrical shape. The ends of the spring are straight, poking out of the cylinder at a certain angle. By pushing on one of the ends (and keeping the other fixed), we obtain a response from the spring. Every device has a defined rate, which allows us to calculate the torque provided by the spring when loaded at a certain angle.
Let's see how to identify the characteristic quantities of a spiral torsion spring and calculate the most important characteristic quantities of such objects!
Calculations for a torsion spring: stress
Torsion springs are the ground for many interesting calculations: but first, let's define the elements of a torsion spring. Take a look at it from the "base" side: you will see a thick circle there we can identify three main quantities:
- The inner diameter of the spring ;
- The outer diameter of the spring ; and
- The wire diameter .
The relationship between these quantities is:
We can also define the average diameter of the spring, :
Knowing this, we can calculate a torsion spring's spring index :
Now let's turn the spring on the side and count the turns. We can identify three types of turns in our coiled torsion spring:
- — The number of body turns;
- — The number of active turns; and
- — The contribution from ends.
You can clearly see these three quantities in the image below.
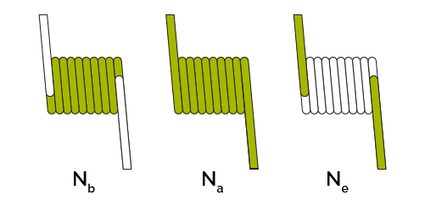
Notice how we can immediately define the first relationship between these quantities just by looking at the image:
To define , we count the complete rotations in the body and sum a contribution of the last incomplete turn (if it's there!):
, either in degrees or radians, is the angle between the extension of the first end and the second end, as you can see in the picture below, where we highlighted the main elements of a spring, seen from above.
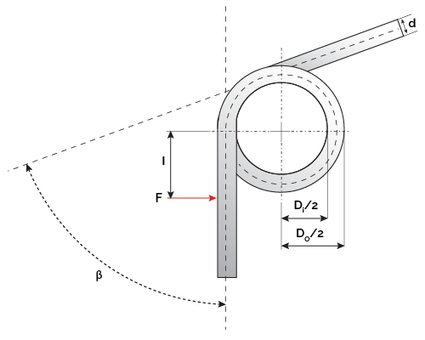
🙋 You can't apply Hooke's law on this type of spring: however, if you are curious, you can still take a look at our Hooke's law calculator!
Calculations for a torsion spring: stress
As the spring bends, the material it's made of is subjected to increasingly intense stresses. The bending stress of a torsion spring depends on the torque applied to one of its ends or equivalently to the force applied at a distance from the center, as you can see in the previous image. The formula to calculate the stress of a torsion spring is:
where:
- — Torque experienced by the loaded spring, we calculate it with the formula ; and
- — Stress correction factor.
🙋 Yup: torque is not only for engines! Learn more about this fascinating physics concept at our torque calculator!
The last quantity is an analytical assessment of the different stress on the spring's wire as it varies between the outside and the inside of the coil. There are two similar formulas to calculate a spiral torsion spring's stress correction factors:
is always larger than , and we use its value when defining the stresses on the round wire.
Knowing the stress experienced by the spring is a fundamental quantity in the design of your machines. However, our calculator for a helical torsion spring doesn't stop here!
How to calculate a torsion spring force, torque, and spring rate
Calculating the force on a torsional spring is even more important than finding the stress. After all, the formulas we are about to see define the behavior of the spring itself when loaded, the expected response, and its "strength". Let's go then!
The first formula calculates a torsion spring's spring rate:
In this equation, we find:
- — Torque, equal to (with the distance from the point of application of the force and the center of the spring, considered parallel to the spring's end); and
- — Angular deflection.
We can express the spring rate either as torque per radian or torque per rotation . The relationship between the two quantities is:
We can calculate a helical torsion spring's angular deflection in radians with the following formula:
where is the Young's modulus of the material: if you need to learn how to find it, don't hesitate to visit our Young's modulus calculator.
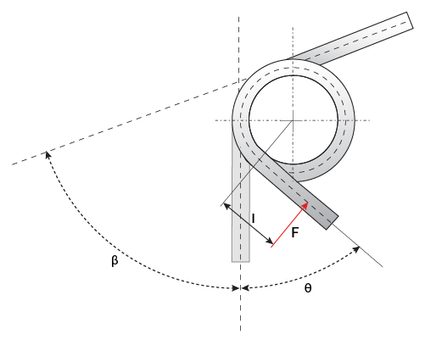
Notice that the spring rate is a constant in the operational range of the spring. Higher torques correspond to higher angular deflection, but their ratio doesn't change.
How to calculate a torsion spring's diameter changes
As the spring bends and increases the number of turns under load, the diameter of the coil decrease. We calculate a torsion spring's new diameter by using the number of body turns:
To find the new diameter of the coil, we calculate the following ratio:
When designing a torsion spring, you may need to coil it around a pivot: in this case, ensure that the inner diameter of your coiled spring at the desired angular deflection doesn't shrink below the diameter of your pivot. The inner diameter of the loaded spring is, of course:
How to use Omni's torsion spring calculator
Fill in the fields of our torsion spring calculator for which you have data, and let us do the math. You can use the helical torsion spring calculator to calculate the size of a torsion spring, knowing the requirements of your device and a bit of the design data (you can find the diameter knowing the number of turns, or vice-versa).
🙋 Omni has a generic tool for other types of springs as well: try our spring calculator to get an overview of springs! And if you need an introduction to how springs store energy, our elastic potential energy calculator will be the right choice!
How to calculate a torsion spring's torque: an example
Let's say that you are working with a steel spring fabricated with the following parameters:
- Wire diameter: ;
- Coil diameter (average): ;
- Number of active turns: ; and
- Young's modulus: .
Let's say that we want our spring to deliver a torque of . How do we calculate the angular deflection of the spring under this requirement? Let's use the angular displacement formula:
With this result, we can calculate the spring rate as the ratio of torque and angular deflection:
FAQs
What is the difference between a helical spring and a torsion spring?
A helical spring works when compressed in the axial direction of the coil and hence operates by providing a force in the direction of the compression. We use this type of spring when linear, straight motions are required.
A torsion spring is used to transmit a torque: the applied force and the returned one are tangential to the coil. This type of spring has many applications in components that rotate.
What is the torque of a torsional spring with rate 0.01 N·m/rad at 45°?
0.0079 N·m. To find this result, we can simply use the relationship which defines the spring rate in a torsional spring:
k = M/θ,
where:
k— Spring rate;M— Torque; andθ— Angular deflection.
Follow these simple steps to calculate the result:
-
Convert the angular deflection into radians:
θ = 45° × (π/180°) = 0.7854 -
To find the torque, multiply the angular displacement by the spring rate:
M = k × θ = 0.01 × 0.7854 ≃ 0.0079 N·m
What is the formula to calculate a torsion spring's stress?
To calculate a helical torsion spring bending stress, we apply the following formula:
σ = K × ((32 × M)/(π × d³)),
where:
σ— Bending stress;K— A correction factor for the stress;M— Torque; andd— Wire diameter.
If you are using metric units, you can calculate the stress in pascals.
How do I calculate a torsion spring's spring rate?
To calculate the spiral torsion spring rate, follow these easy steps:
-
Measure the angular deflection of the spring,
θ. You can do this either in radians or in turns (1 turn = 2π radians). -
Measure the torque applied by the spring
M. -
Divide the torque by the angular deflection. The result is the spring rate
k:k = M/θ. -
If you are computing the spring rate in
N·m/radand want to know its value inN·m/turn, simply multiply thekby2π.