Spring Calculator

The handy spring calculator expresses the relationship between the force or torque applied to a spring and its deformation. This article will show you how to use this Omni Calculator spring compression tool. Also, we will cover what the spring compression formula is and how to calculate the spring constant for different configurations. Keep reading to understand this amazing mechanism that has been used for a long time.

A spring is a mechanical device that stores energy while deforming its shape when a force or torque is applied. If you want to know specifically which type of energy, check the elastic potential energy calculator.

There are several types of springs; however, in this spring calculator, we will cover the three main types of springs. Its categorization depends on the direction of the external force or if torque is being applied. Such types are:

• Compression springs: Springs that are designed to work under a compression force.
• Expansion springs: Springs that are designed to work under a traction force.

In both cases above, the spring compression formula applies but in different directions, as you will see in further sections. Also, both follow the same behavior as the one explained in Hooke's law calculator.

• Torsion springs: These are springs that experience momentum due to a force that is being applied outside of the center of gravity of the spring, specifically in one of the spring legs. Such force would make the spring rotate if we did not fix the other leg. Since the spring does not rotate, it deforms because of the torsional force, and it stores energy like the other springs.

Although any spring follows the same principle as the energy conversion calculator, expansion/compression springs and torsion springs have different formulas. In this section, we will cover the equation for the force of a spring:

where:

• $F$ — Force – represents the force that reacts to the compression or compression of a spring, measured in Newtons;
• $k_{\rm tc}$ — Spring constant for traction or compression – indicates the linear relation between the change in spring length and the force applied. It is measured in Newton/meter; and
• $\Delta x$ — Spring change in length due to the force applied. It is measured in meters (positive for elongation and negative for compression).

Furthermore, if we want to buy some springs, we need to specify more detailed information. You might have already guessed that the spring constant should also be related to its shape. Indeed, the compression of a spring that is thicker than another is much more complicated if we assume we are dealing with the same material.

The following equation relates material properties and geometrical shape in an equation that is called: the spring rate formula:

where:

• $G$ — Shear modulus - Also known as modulus of rigidity, it measures the elastic shear stiffness of a material. You will typically find its values expressed in GPa.
• $d$ — Wire diameter - Represents wire thickness.
• $D$ — Mean diameter - The mean diameter indicates the size between the outer and inside diameter.
• $N_{\rm a}$ — Number of active coils - Indicates the number of coils that are working when the spring is under load.

See the next picture for further details:

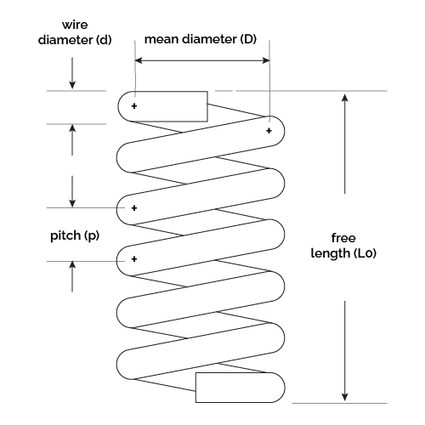
Give a check to the Free length $L_0$ and Spring pitch ($p$) on the image above since we are going to cover them in further detail below.

Our excellent spring calculator includes all the details you would need for designing a spring; however, there are three design parameters we have not explored:

• Spring index ($C$): Mathematically, it is the relation between the mean spring diameter $D$ and the wire thickness $d$: $C = D/d$. Manufacturers and spring users utilize it to define the manufacturability of a spring. Usually, a spring with a spring index between 5 and 10 represents an easy/not costly spring to manufacture.

• Free length value of a spring ($L_0$) refers to the spring length with no load.

• Spring pitch ($p$): Refers to the space between two adjacent coils and is directly related to the free length value ($L_0$) of a spring.

There is a last design parameter but similarly to the pitch, it only matters to expansion/contraction springs:

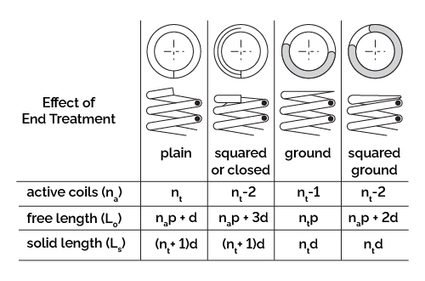
• Spring end type: This property refers to how are the external faces of a spring. We have included four types: grounded, squared, plain, and squared & ground.

We have to do a further step in explaining "how to calculate spring force" in the case of a torsion spring.

First, we start with the momentum we apply to the spring:

where:

• $M$ — Torque – Torque represents the rotational equivalent of a linear force. It is expressed in Newton meters.
• $k_{\rm torsion}$ — Spring constant for torsion – Indicates the relation between the spring twist and the momentum applied. It is measured in Newton meters per radian.
• $\alpha$ — Twist angle – Represents the achieved angle while twisting the spring. It is expressed in radians.

Once we get the momentum, we need the length of the distance of lever arm $r$ (distance between the force applied and the center of rotation of the spring) and by solving the following equation:

We get the force ($F$) applied to a torsion spring.

Finally, we will cover the design spring equation:

where:

• $k_{\rm torsion}$— Torsional spring stiffness, in N·m/rad;
• $E$ — Elasticity modulus – Represents the material resistance to being deformed elastically. Usually expressed in GPa.
• $d$ — Wire diameter, in m;
• $D$ — Mean coil diameter, in m; and
• $N_{\rm a}$ — Equivalent number of active turns (dimensionless).

See the next picture for further details.

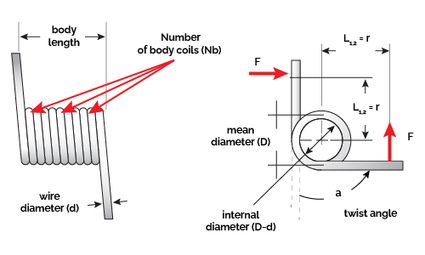
We obtain $N_{\rm a}$ with the number of body coils $N_{\rm b}$) and the lengths ($l_1$ and $l_2$, expressed in meters) of the ends where the torsional force is applied:

Note from the picture above that at least one of $l_1$ and $l_2$ will be the length of the distance of the lever arm $r$ because it represents where the torsional force is applied. The other could be the same but also could vary.

Let's assume you need an expansion spring for a 20-kilogram load. You need it to have a maximum extension of an extra 20 cm, be made of stainless material, and have a maximum outer diameter of 4 cm. The parameters we need to obtain are the number of active coils and the spring pitch.

Try the spring calculator for different spring indexes ($C$) and free length values ($L_0$). In this example, we will consider 9 and 20 cm, respectively.

1. Let's define the information we have. According to the spring formula, we have $F = 196.2\ \rm N$, and $x=0.2\ \rm m$. That means we have a spring coefficient equal to $k_{\rm tc} = 981\ \rm N/m$.

2. Let's choose a spring index of 9 because of its manufacturability and a maximum outer diameter of 0.04 m. Such spring index indicates a mean diameter $D$ nine times spring wire thickness $d$. Considering the outer diameter, we get a spring thickness of 4 mm. Hence a mean diameter of 36 mm.

3. Now, we proceed to get the number of active coils by using the spring rate formula:

Solving the equation considering $G = 77\ \rm GPa$ returns 53.83 ~ 54 active coils.

4. Finally, if we need it with plain ends and a free length of 20 cm, we get a pitch of 3.64 mm.