Combined Gas Law Calculator

This combined gas law calculator is a great tool to deal with problems related to the most common transformations of gases. Read about isobaric, isochoric, isothermal, and adiabatic processes of ideal gases (gases that can be described by the ideal gas equation) and how the ideal gases can do work or release/absorb heat.

Check out the exact values for real gases using our van der Waals equation calculator, and forget about struggling with thermodynamic exercises!

We can describe an ideal gas can by several parameters: pressure p, volume V, temperature T, and the number of particles n. It's possible to correlate them with the equation: p·V = n·R·T, where R stands for ideal gas constant and equals 8.3144598 J/(mol·K).

During any process, at least two of these properties change, which we can compile into the combined gas law formula: p·V/T = k, where k is a constant.

Out of all transformations, we can distinguish a few which encompass a vast majority of examples from everyday life, or we can treat them as good approximations.

In this combined gas law calculator, we consider processes in which the number of particles is constant. Thus we can imagine a gas in a closed container. These are:

• Isochoric process;
• Isobaric process;
• Isothermal process; and
• Adiabatic process.

Internal energy U is the sum of all kinds of energy present in a system. It's quite tricky to estimate the precise value of internal energy. Still, it is possible to find thermal energy changes ΔU, which are described by the first law of thermodynamics: ΔU = Q - W, where Q denotes heat absorbed, and W is work done by gas.

Internal energy change is proportional to temperature variation ΔT and type of gas with the following equation: ΔU = Cv·n·ΔT, where Cv is molar heat capacity under constant volume. For an ideal gas, it takes values:

• 3/2·R for monoatomic gas;
• 5/2·R for diatomic gas; and
• 3·R for gases with more complex molecules.

These parameters in real gases differ from theoretical ones, but we already contain them in our thermodynamic processes calculator.

The general formula for work done by the gas is expressed as ∫p(V)dV if we consider pressure as the function of volume. Although it isn't trivial in general, you can check how the formula simplifies for processes mentioned below.

During this transition volume is a constant parameter, so that initial properties p₁, T₁ changes to p₂, T₂ as follows: p₁ / T₁ = p₂ / T₂.

The invariability of volume means that the gas doesn't do any work and the heat absorbed by gas is precisely the same as internal energy change: ΔU = Q = Cv·n·ΔT. We can visualize this process for gas kept in a rigid container that can exchange heat with an environment. You can try our Gay-Lussac's law calculator, as Gay-Lussac's law corresponds to this thermodynamic process.

We assume that pressure is a constant gas parameter during this transition. Therefore the initial parameters V₁, T₁ transform to V₂, T₂ with the following form of combined gas law formula: V₁ / T₁ = V₂ / T₂.

Since pressure is invariant, the formula for work done by the gas is W = p·ΔV. Heat, however, can be calculated as: Q = ΔU + W = Cv·n·ΔT + p·ΔV = Cp·n·ΔT.

Cp is known as molar heat capacity under constant pressure, and for an ideal gas, it is associated with Cv, so that Cp = Cv + R. Check Omni's Charles' law calculator, as Charles' law is related to isobaric transition.

The constant parameter in this transition is temperature so that initial properties p₁, V₁ change to p₂, V₂, and the correlation is: p₁·V₁ = p₂·V₂. In the presented example, we can see that, according to the ideal gas equation, the pressure is the following function of volume: p(V) = n·R·T / V = A / V, where A is constant throughout the whole process.

We can estimate the general expression for work done by the gas as W = n·R·T·ln(V₂ / V₁), where ln stands for the natural logarithm of a given number. Due to the temperature constancy, initial energy doesn't change, which implies the equality: Q = W. One can say that we transform the entire heat absorbed by gas to work done by it, but on the other hand, this transition is known to be very slow in practice. For a more detailed explanation, head to our Boyle's law calculator, which describes thermodynamic processes of this kind.

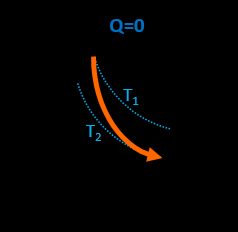
In this transition, all three parameters change, but simultaneously the gas doesn't exchange heat with the environment. The following formula is valid: p₁V₁^γ = p₂·V₂^γ, where γ = Cp / Cv is known as heat capacity ratio. The work done by the gas is opposite to its initial internal energy change W = -ΔU. This process describes transitions that progress rapidly, and there is no time for the gas to absorb or release any heat.

Let's assume that you want to find the internal energy change, the heat absorbed and the work done by nitrogen stored inside a flexible container of volume 0.5 m³ under atmospheric pressure and at temperature 250 K, which we heat up to 300 K. In this case, we consider an isobaric process.

1. Calculate the final volume:

   V₂ = V₁·T₂ / T₁
   = 0.5 m³ · 300 K / 250 K
   = 0.6 m³

2. Work out the number of molecules:

   n = p·V₁ / (R·T₁)
   = 101.325 kPa · 0.5 m³ / (8.314 J/(mol·K) · 250 K)
   = 24.375 mol

3. Find the heat capacity Cv of nitrogen, which is 20.814 J/(mol·K) (for ideal diatomic gas, it should be equal to 20.786 J/(mol·K)).

4. Estimate internal energy change:

   ΔU = 20.814 J/(mol·K) · 24.375 mol · 50 K
   = 25.367 kJ

5. Determine the work done by gas:

   W = 101.325 kPa · 0.1 m³
   = 10.133 kJ

6. Evaluate the heat absorbed by nitrogen:

   Q = 25.367 kJ + 10.133 kJ
   = 35.500 kJ.

You can always save your time and use our combined gas law calculator!

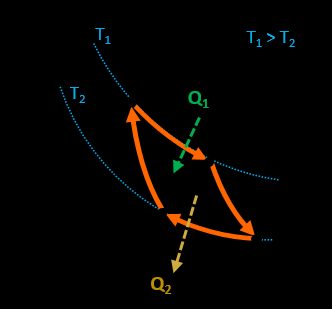
This is one of the cycles representing the model of an ideal engine with the highest efficiency possible in the mean of thermodynamic laws.

Our Carnot efficiency calculator covers the topic exceptionally well! It consists of two adiabatic and two isothermal processes. This engine absorbs heat from a hot reservoir, transforms it into work, and releases the rest of the heat to the cold one.

With this combined gas law calculator, you can design any kind of thermodynamic cycle and find out how this change influences output efficiency!