Carnot Efficiency Calculator

If you're interested in thermodynamics, you should definitely give this Carnot efficiency calculator a try. It is a handy tool that helps you determine the thermal efficiency of an engine operating on the Carnot cycle. Continue reading to find out what the Carnot cycle is, how to solve a Carnot efficiency equation, and why you shouldn't use this type of engine in your car.

A Carnot heat engine operates on the Carnot cycle, the most efficient heat engine process allowed by the laws of thermodynamics. In this cycle, the engine goes through four consecutive processes and returns to its initial state afterward.

The engine itself consists of two stationary bodies and a working substance (a fluid or a vapor body). The two stationary bodies have constant temperatures:

• The first one (called a "furnace") has the high temperature $T_\text{h}$.
• The second one (called a "refrigerator") has the low temperature $T_\text{c}$.

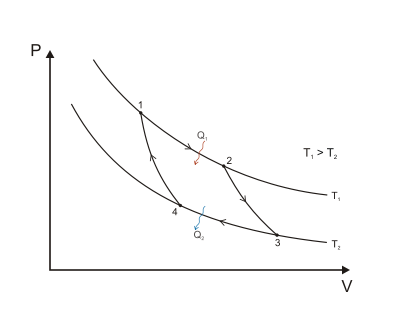
The four phases of a Carnot cycle are:

1. Isothermal expansion at $T_\text{h}$. The working substance expands at the constant temperature $T_\text{h}$, performing work on the surroundings.

2. Adiabatic expansion. The working substance expands further, doing work on the surroundings, but loses a part of its internal energy. Loss of energy means cooling down to the temperature $T_\text{c}$.

3. Isothermal compression at $T_\text{c}$. The surroundings perform work on the working substance, compressing it at a constant temperature $T_\text{c}$. As the pressure is lower than in Step 1, the amount of work is smaller than the work generated back then.

4. Adiabatic compression. The surroundings continue to work on the working substance, compressing it further. The compression results in an increase in temperature to $T_\text{h}$. At the end of Step 4, the working substance is precisely in the same state as before Step 1.

The Carnot engine is the most efficient heat engine that can be built. To find its efficiency $η$, you need to apply the following equation:

Both $T_\text{h}$ and $T_\text{c}$ are absolute temperatures (expressed in Kelvins).

For example, you can try to calculate the Carnot efficiency of an engine operating between two bodies: one at a temperature of $25\text{ °C}$, and the other at $135\text{ °C}$. To find the result, you need to follow these steps:

1. Use the temperature converter to convert $25\text{ °C}$ to Kelvins. You can also do the calculations manually — in this case:

2. Repeat step 1 for the temperature of the hot reservoir. In this case:

3. Input these values into the Carnot efficiency equation:

4. The Carnot efficiency is equal to 26.95%. You can verify the result with our thermal efficiency calculator!

The Carnot engine is an idealized case of a heat engine. Nevertheless, it would be theoretically possible to build an engine using the model of two reservoirs with constant temperatures and a working substance.

The reason why the engine has no practical application is the duration of each process. Isothermal processes are awfully slow, and it would take enormous amounts of time before the heat transfer actually occurs. As Schroeder concluded, "don't bother installing a Carnot engine in your car. While it would increase your gas mileage, you would be passed on the highway by pedestrians."