Coefficient of Performance Calculator

Governments worldwide have established standards to encourage energy efficiency, and calculating the coefficient of performance of refrigerators and heat pumps becomes crucial to know if we're accomplishing those standards.

You can do it with this tool, a calculator that will let you calculate the coefficient of performance of heat pumps and refrigerators (either reversible or irreversible), or use the coefficient of performance formulas presented below in this article.

The coefficient of performance (COP) is one of the most common ways to quantify the efficiency of refrigerators and heat pumps.

As we mention in the efficiency calculator, in a broad sense, the efficiency of a machine is the ratio of energy output to energy input. The energy output is the desired quantity to accomplish an objective, while we can see the energy input as the "cost" to pay for it.

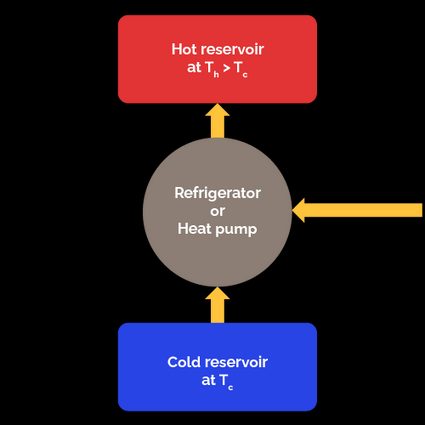
Refrigerators and air conditioners are machines that accomplish an objective, and we can identify their inputs and outputs:

• For a refrigerator, the "output" or desired effect is the amount of energy (heat) we remove from the space to refrigerate. The input is the work we must provide to the refrigerator to accomplish its task.

• For a heat pump, the "output" is the amount of energy we supply to the high-temperature space, and the input is the work we must provide to the heat pump.

With a refrigerator, we remove an amount of heat $Q_\text{c}$ from a refrigerated space at a temperature $T_\text{c}$. To achieve this, we must apply work $W$ to the refrigerator. The heat the refrigerator receives ($Q_\text{c}$) plus the energy in the form of work we apply to it ($W$) are rejected to the warm environment at a temperature $T_h$. According to the first law of thermodynamics, the amount of head rejected is $Q_\text{h} = Q_\text{c} + W$.

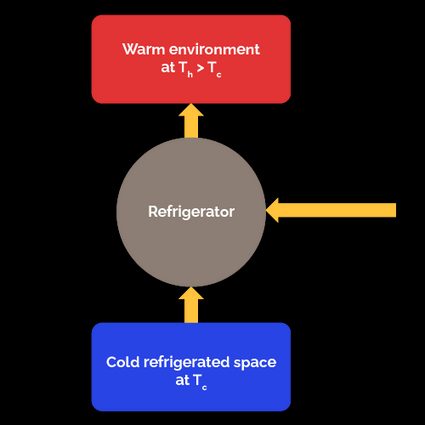
The COP of a refrigerator is the ratio of the heat removed from the refrigerated space to the required work input necessary to do it:

Considering that $Q_\text{h} = Q_\text{c} + W$, we can express the COP of the refrigerator in terms of only the two heats:

A heat pump works the same way as a refrigerator, but with a different objective: our goal is to heat a warm space instead of refrigerating a cold one. Therefore, our desired output is the heat we transfer to the high-temperature space to keep it warm. Then, the COP of a heat pump is:

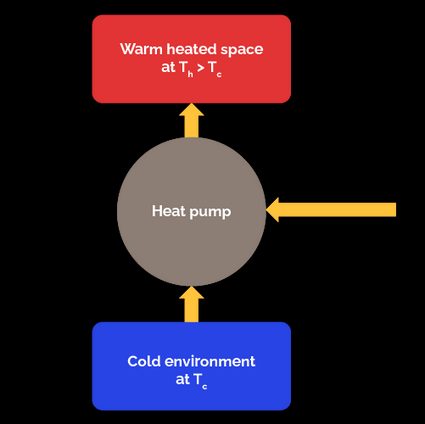
Comparing the $\text{COP}_ \text{hp}$ and the $\text{COP}_ {\text{r}}$ formulas, for fixed $Q_\text{c}$ and $Q_\text{h}$ values, we can note the following relationship:

The previous relationship indicates that, at least in theory, the COP of a heat pump should always be greater than one. However, it could be lower than that if $T_\text{h}$ is so low that a significant part of $Q_\text{h}$ is lost to the environment through piping and other devices. When this occurs, the system switches to resistive heating mode to warranty a $\text{COP}_\text{hp} > 1$.

Just like heat engines, refrigerators and heat pumps operate on cycles, but their function is the opposite:

• Heat engines absorb heat from a high-temperature source and reject part of it to a low-temperature sink, all intending to produce work.

• On the other hand, refrigerators and heat pumps take heat from a low-temperature reservoir and reject it to a high-temperature one, requiring some work to achieve it.

As we explain in the Carnot efficiency calculator, the Carnot heat engine is a theoretical heat engine that operates under the Carnot cycle, the most efficient heat engine process possible. This maximum efficiency of the Carnot cycle occurs by executing it as a reversible process (no irreversibilities).

Because the refrigeration cycle is the reversed version of a heat engine, we can also execute the Carnot cycle in a reversed way and obtain a Carnot refrigerator or heat engine. The COP of reversible refrigerators or heat pumps is the same as that of the irreversible versions of the previous sections:

Even so, if we use the second Carnot principle and the Kelvin thermodynamic temperature scale, it can be shown that the Carnot COP (like the Carnot efficiency) is only a function of the cold and hot reservoir temperatures:

Like the Carnot efficiency, the Carnot COP is the maximum possible COP a refrigerator or heat pump can achieve for a couple of cold and hot reservoir temperatures.