RMS Voltage Calculator

Welcome to the RMS voltage calculator, with which you can quickly calculate the RMS of common waveforms. We'll learn about topics such as what RMS voltage is, the general equation for RMS voltage, and how to calculate RMS voltage for your favorite waveforms. Let's charge ahead!

Get it? "Charge"? As in "electrical charge"...? ... I'll see myself out.

Before we can talk about waveforms and their RMS values, we first have to examine the RMS and what it represents. The root mean square of a series of numbers is the root of the mean of the sum of their squares. RMS is also known as the quadratic mean. So, for:

our RMS value $Y_\text{RMS}$ would be:

The RMS isn't just an average of the numbers; it's an entirely separate concept with valuable properties, which we'll learn about in the rest of this article.

Most real-world waves and signals are continuous-time functions. When we deal with these, the equation for the root mean square changes somewhat. We're also only considering periodic functions for this calculator. A periodic function is a function that repeats its values at regular intervals. We denote such a function's period with the symbol $T$. Trigonometric functions are great examples of periodic, continuous-time functions — both sine and cosine waves' period is $T = 2\pi = 360^\circ$. A periodic function's RMS over one of its periods is the same as its RMS over its entirety. We can obtain the RMS of a periodic, continuous-time waveform $y(t)$ with:

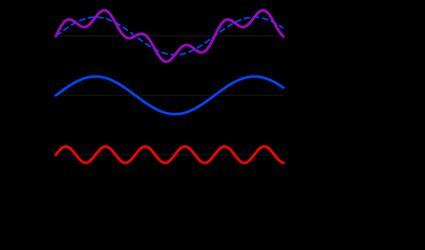
A periodic, continuous-time function can be expressed as the sum of smaller functions with the same period. We can denote it as $y(t) = y_1(t) + \dots + y_N(t)$. If we need to calculate $y(t)$'s RMS value $Y_\text{RMS}$, we can combine the components' individual RMS values as follows:

Here's a visual representation of what's happening:

When working with AC voltages, the RMS takes on a special meaning. The RMS of an alternating electric current represents the value of a direct current that would dissipate the same electrical power in a load as the alternating current does. Knowing the RMS of an AC waveform allows us to determine how much power is dissipated in the load, and because AC is much more prevalent in electrical systems than DC, this is a wonderful tool for your engineering toolbox.

If we have a periodic AC voltage, we'd denote it as $v(t)$. Ultimately, we want to calculate $V_\text{RMS}$, which is $v(t)$'s equivalent DC voltage. Since $v(t)$ is continuous and periodic, we can use the formula for continuous-time, periodic functions that we learned about before.

Our RMS voltage calculator takes care of all the pesky formulas for you. To get your waveform's RMS in a zap ⚡ follow these easy steps:

1. Select your waveform shape. Our RMS voltage calculator lets you pick between sinusoidal, square, sawtooth, and triangular waves, as well as half- or full-rectified sine waves.

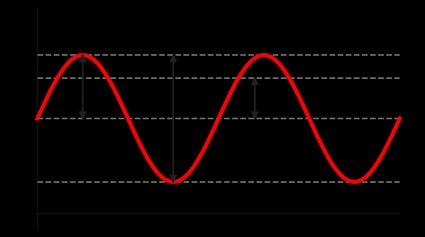
2. Select your waveform's characteristic voltage. You can choose to input $V_\text{p}$, $V_\text{pp}$, or $V_\text{avg}$ as indicated on the diagram at the top of the calculator.

3. Enter the waveform's characteristic voltage (the value for $V_\text{p}$, $V_\text{pp}$, or $V_\text{avg}$) and offset $V_0$.

4. Find your RMS voltage in the last row of the calculator. You can also use the RMS voltage calculator backward and let it find the characteristic voltage or the DC offset if you know the RMS voltage and the remaining value.

We've learned what the RMS voltage is and watt 💡 the fuss is all about, but how do we calculate the RMS for common waveforms? While we saw the universal RMS voltage equation above, the most common waveforms have unique formulas derived from our universal RMS voltage formula. The answer to this question depends on a few things:

• The waveform shape (sine wave, square wave, etc.);

• The characteristic voltage of the waveform ($V_\text{p}$, $V_\text{pp}$, or $V_\text{avg}$) and its value; and

• The DC offset of the waveform, $V_0$.

The waveform shape and characteristic voltage determines the RMS voltage formula we need to use. We've collected some common waveforms and their RMS value formulas in the handy table below. These RMS voltage equations do not take DC offsets into account yet — read on to learn how we deal with those!

But where does the offset voltage, the waveform's DC component, $V_0$ fit in? If you think back at what we learned so far, you'll remember how to calculate the RMS of a function that is the sum of same-periodic continuous-time functions:

We can leverage this property to account for $V_0$ when calculating the RMS of the waveform $v(t)$. For example: from the table above, we know that $V_\text{RMS} = V_\text{p} / \sqrt{2}$ for a sine wave with no DC offset. When a DC offset $V_0$ is added to the sine wave, we can determine our new RMS value with