Manometer Calculator

This manometer calculator will help you determine the hydrostatic pressure in a fluid using a manometer. This article also answers questions like "How does a manometer work?," "How to use a manometer?", and much more. Read on to learn about Pascal's Principle and to discover what manometers and U-tube manometers are. We'll also show you some examples with the manometer equation to help you easily grasp the physics behind this handy device.

A manometer is a scientific instrument used to measure fluid pressure, such as in gases and liquids. A manometer is a simple tool made of a uniform diameter glass tube attached to a reservoir or a pipe. A manometer could also be just a tube that is used to measure atmospheric pressure and pressure difference caused by fluids interacting with each other. A manometer usually contains a high-density liquid like mercury. Manometers can also be filled with water, oil, or any liquid, as long as we know its density or specific gravity. In certain applications, manometers may also contain multiple liquids.

Now that we know what a manometer is, let us discuss how a manometer works. Manometers work by following Pascal's Principle. You can learn more about Pascal's Principle by checking out our hydraulic pressure calculator. Pascal's Principle states that:

"pressure applied to any part of an enclosed incompressible liquid will be transmitted equally in all directions through the fluid."

To better understand Pascal's Principle, think of a toothpaste in a tube. Squeezing the tube's body transmits pressure throughout the toothpaste until the toothpaste oozes out of the nozzle. The amount of squeezed out toothpaste is the result of the amount of pressure applied to the tube.

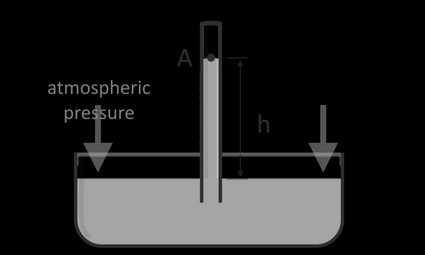
If we installed a manometer like a u-tube manometer at the nozzle of the toothpaste tube and squeeze it again, the toothpaste will travel through the manometer at a certain height, h, as shown below:

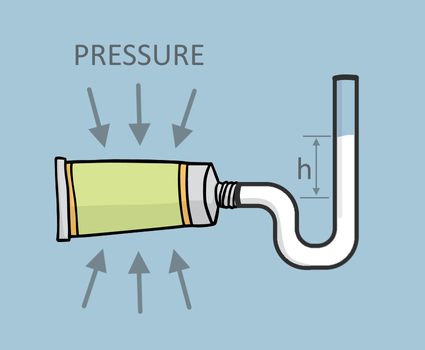
We can calculate the pressure that we applied on the toothpaste tube using the hydrostatic pressure equation

where,

• $P$ is the pressure the liquid (toothpaste) experiences at height $h$;
• $\rho$ (Greek letter rho) is the liquid's density; and
• $g$ is the gravitational acceleration of 9.806 m/s² (or approximately 32.174 ft/s²).

Pascal's Principle then goes on to say that the pressure around the toothpaste tube is equal to the toothpaste pressure at the given height. We can then say that the hydrostatic pressure equation is also the manometer equation.

Let's say that toothpaste density is 1.3 g/cm³ (which is equivalent to 1,300 kg/m³), and h is 5.0 cm (or 0.05 m) from the nozzle of the tube. Substituting the values that we have into the manometer equation, we now have a calculation for the pressure on the toothpaste tube:

A manometer is as simple to use as our toothpaste example. Just like what we did there, we could also attach the manometer to pipes or other conduits and vessels that experience fluid pressure. We can install a manometer along a pipe to determine the pressure of the water that flows through the pipe. However, if the pressure in the pipe is enormous, the liquid passing through it could squirt out of the manometer. We can use very large and long manometers, but they can be costly and difficult to read. Instead, we can introduce a high-density liquid in the manometer to regulate h. The denser the fluid is, the higher pressure it can support, and the lower h it produces.

Manometers with multiple fluids require us to calculate the sum of all the pressures caused by each liquid column in the manometer. Let us consider an example to understand this concept. Suppose we have a u-tube mercury manometer attached to a pressurized pipe. The movement of the liquid inside the pipe results in a pressure that we want to determine. As the liquid flows through the pipe, liquid gets inside the manometer. The liquid pushes the mercury to a certain level, as shown below:

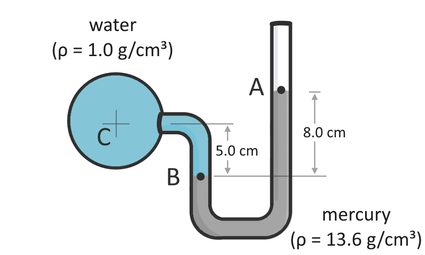
In this example, we have mercury (ρ₁=13.6 g/cm³ or 13,600 kg/m³) and water (ρ₂=1.0 g/cm³ or 1,000 kg/m³) in the system. Water flows through the pipe, and mercury is the high-density fluid inside the manometer. The height difference between points A and B (which we can denote as h₁) is equal to 8.0 cm (or 0.08 m). On the other hand, the height difference between points B and C (h₂) is equal to 5.0 cm (or 0.05 m). Given this information, we can now solve for the pressure in the pipe at point C, P, as follows:

From the calculation we have above, we can say that the pipe pressure is equal to 10,178.628 Pascals or 10.18 kPa. In this example, notice that we negated the pressure $\rho _ 2 \,g \, h_2$ from the equation. We did this because whenever we calculate for the pressure at a point higher than the first point we consider, the pressure at the second point must always be lower than the pressure at the first point. Imagine being in a deep swimming pool. As you go deeper, you will feel more pressure from the water surrounding your body because more water is above you. The weight of the water causes you to feel more pressure as you go deeper. This concept is also true with air, and you can learn more about this in our air density calculator

In this manometer calculator, you have a selection of typical manometer shapes and uses. Then, you have to input the densities and height differences of the points shown in the calculator's diagrams.

Most manometers come with graduations, making it easy to determine the water columns' heights. Just remember first to calibrate the manometer using another pressure measuring device. Calibration ensures that the measurements we obtain using our manometers are standard measurements and are reliable.

If you want to learn more about the laws and principles of fluids, gases, and liquids, you might want to visit our Boyle's Law calculator, Charles' Law calculator, and Gay-Lussac's Law calculator.