Inverse Square Law Calculator

The inverse square law calculator will help you understand one of the basics laws governing our universe. In this article, you will learn:

• What is the inverse square law?
• How to calculate the inverse square law formula in a generic situation.
• Examples of the inverse square law in Nature: calculating the inverse square law for radiation and other phenomena.
• How to use our inverse square law calculator.

And much more. What are you waiting for? Let's dive into the relationship between geometry and the physical world!

The inverse square law describes how physical quantities radiating from point sources dissipate as a function of the distance. The core concept is that if the emission is radial, we can map it on a spherical surface. The radius of the sphere corresponds to the distance from the point source.

We calculate the area of a sphere as it grows according to the formula:

where we find a dependency over the square of the distance rather than on the distance itself.

Imagine turning on a lightbulb inside a deflated balloon (don't do it if the bulb is prone to get hot!). The bulb emits light with a given luminous flux measured in lumens. This flux distributes on the skin-tight (bulb-tight?) balloon with a specific illuminance (luminous flux per unit area) that equals the flux divided by the area of the balloon itself.

Now inflate the balloon so that it roughly approximates a sphere with a given radius $r$. How did the quantities we introduced above change?

• The luminous flux remained the same since we are not "missing" out on any bit of radiation emitted by the bulb.
• The illuminance is reduced by a factor controlled by the change in the surface area of the balloon.

This means that, while we are catching all the energy emitted by the bulb, every unit area on the balloon receives less energy than before.

In jargon, we call this characteristic behavior of radiating phenomena geometric dilution, as the power of the source per unit area reduces with the distance.

This section introduces you to a generic formula for the inverse square law. This formula takes away all the physicality of a problem while maintaining the concept of geometric dilution. Take a point source that emits with an intensity $I_1$ at a distance $r_1$. We can use the idea of geometric dilution to relate these two quantities and find other pairs of intensity and distance according to the following equality:

which is to say that the product of intensity and square radius is constant:

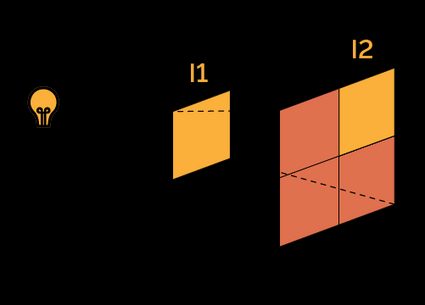
The intensity, in this equation, can be anything. Where do we find the inverse square law in our physical world?

We already gave you an example of propagation that follows the inverse square law: light from a point source. Light from the stars dilutes as a function of the distance simply following the formula for the inverse square law. We can calculate the inverse square law for radiations of every kind: visible light is only one of them.

But the inverse square law doesn't stop at light. Let's discover other phenomena that follow the same property!

• Gravitational force. Newton noted in his seminal paper on gravitation that the gravitational force appears to be inversely proportional to the square of the distance between two bodies: you can discover more about this fundamental force at our gravitational force calculator. The formula for the gravitational force puts this assumption in mathematical terms:

• Electric field. The electric field emanated by a point charge propagates in space according to the inverse square law when we calculate Coulomb's law formula. The formula is much similar to the one Newton found for the gravitational force, and we can't help but marvel at the parallels between such different phenomena:

• Sound. While we perceive sound as logarithmic in our brains, its propagation follows the inverse square law.

• Shock waves are a peculiar type of sound characterized by a speed higher than the local speed of sound. Nevertheless, their propagation follows the inverse square law: better be far enough from the detonation!

Our inverse square law calculator allows you to calculate the propagation of any generic phenomena that follows the same geometrical evolution. For this reason, we didn't specify any units for the intensity field, leaving you the decision. We added a scientific notation converter that may be useful if the values become too big or too small.

Let's try our hand with a practical example! Let's take the solar irradiance at the top of Earth's atmosphere. This value is well known and assessed at $1361\ \mathrm{W/m^2}$. This is the $I_1$ of our example. What about $r_1$? $r_1$ is the average distance between Earth and Sun, about one astronomical unit or $149,\!597,\!871\ \mathrm{km}$. Better keep it expressed in $\mathrm{UA}$.

What is the value of the irradiance at the surface of Mars? This value would be $I_2$. Luckily, we have a good approximation of $r_2$, the average distance between Sun and the red planet: $r_2 = 1.53\ \mathrm{AU}$. Plug these values in the calculator for the inverse square law formula. It will perform the following operation:

That's less than half of what Earth receives. No wonder Mars is pretty cold (it's not the only reason, though)!

The inverse square law is a physical law that describes the propagation of quantities inversely proportional to the square of the distance from the source. Quantities that propagate in a radial fashion from point sources are most likely to obey the inverse square law, as the total throughput dilutes on the surface of a sphere, that in turn evolves according to the formula A = 4πr². The square of the distance appears thanks to this formula.

The propagation of light from a point source (or a good approximation of it) is a perfect example of a phenomenon that obeys the inverse square law: as a light source's power remains constant, we dilute it on the surface of the sphere, defining a quantity we call illuminance. The illuminance depends on the unit area, and obviously, it decreases as you get farther from the source.

To calculate the inverse square law, you need to know three of these four elements:

• The intensity I₁;
• The distance from the source r₁;
• The intensity I₂; or
• The distance from the source r₂.

Once you have selected the desired quantities, use the following equality to derive the missing element:

I₁/I₂ = r₂²/r₁²

According to the inverse square law, we can compute the reduction in intensity corresponding to an increase of the distance from 1 to 3 meters following a few simple steps.

1. Calculate the ratio of the square of the distances: 1²/3² = 1/9 = 0.11.
2. This result is the reduction factor: multiply the intensity associated with the distance 1 meter to find the intensity at the distance 3 meters.