Impact Test Calculator

The impact test calculator will help determine the energy absorbed by a notched material specimen. We perform impact tests to understand material failure behavior in dynamic conditions.

Structures for transportation, military, and space applications undergo extreme loads while operating. The materials for such structures must be tested for their fracture toughness and failure to understand how they would deform and ultimately break under the said dynamic conditions like impact or shock loads.

Some examples of impact loads are an object falling on the ground, a vehicle crash (refer to our car crash calculator for more), bird strikes on the windshield, etc. Some typical impact tests are pendulum-based tests like Charpy and Izod impact tests. These tests follow different standards for plastics, metals, composites, and concrete.

This article covers the energy absorption calculation you need after performing an Izod or a Charpy impact test. Read on to understand what an impact test is and how to calculate energy absorption.

An impact test consists of a striker hitting the test specimen to transfer a large force in a short time. You can use a drop tower or a pendulum tester to achieve such large forces.

A striker is dropped vertically from a height for a drop tower test and uses gravity to achieve the necessary impact energy. Similarly, in a pendulum test, the striker is fixed to an arm that swings like a pendulum. There are two pendulum tests: Izod and Charpy impact tests.

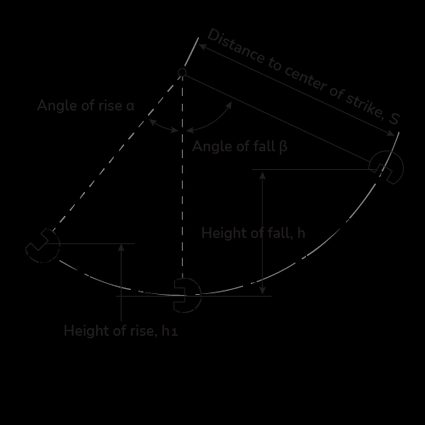
The test begins with the arm set to a high position at the angle of fall, $\beta$. The pendulum, upon release, travels from the height, $h$, such that it swings and makes contact with the notched specimen. Whenever a moving striker stops suddenly due to a collision, it transfers its kinetic energy to the material specimen. The sample deforms upon impact, generating a stress wave in the form of body and surface waves.

The specimen elongates (check out our elongation calculator). The striker rises again to a certain angle, i.e., angle of rise, $\alpha$. Let $h$ be the initial height of the hammer or striker. Such that, for an arm of length, $S$, the initial height is:

Similarly, the maximum height ($h_1$) of the striker after the collision is:

The dissipated energy during an impact test, $E$ becomes:

Here, $E_l$ refers to the energy loss. As per ASTM D256, some examples of energy loss are:

• Energy dissipated to produce vibration in pendulum arm or horizontal movement of the machine frame or base;
• Energy loss due to friction in pendulum bearing and indicating mechanism;
• Energy loss due to rubbing of the striker over the face of bent specimens; and
• Energy loss due to windage or air drag.

To estimate the energy losses, you can perform the test with no target and evaluate the pendulum's energy on either side of the specimen position.

The above energy formula is applicable for pendulum tests. Now let's look at the two types of impact tests:

1. Izod impact test; and
2. Charpy impact test.

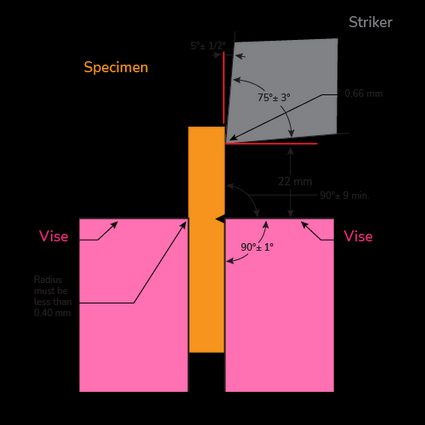
The Izod test is a pendulum-based impact test named after an English engineer, Edwin Izod. The sample is held vertically as a cantilever beam and is struck with a hammer attached to a pendulum. The test gives us the impact resistance of the material. The test is conducted per the ASTM standards D256 and D4812 for notched and unnotched specimens, respectively.

The samples are notched to achieve higher stress concentration, increasing the probability of a brittle failure. The notch minimizes the plastic deformation and directs the fracture toward the material behind the notch.

As per the testing standard ASTM D256, four failure scenarios could occur to the specimen — complete break, hinge break, partial break, or non-break.

Complete Break (C) — Specimen separates into two or more pieces.

Hinge Break (H) — Incomplete break, such that one part of the specimen cannot support itself above horizontal when you hold the other part vertically.

Partial Break (P) — An incomplete break that has fractured extends no less than 90% of the distance from the vertex of the notch to the opposite side.

Non-Break (NB) — An incomplete break where the fracture extends less than 90% of the distance between the vertex of the notch and the opposite side.

The Charpy test is a pendulum-based test introduced by Georges Charpy and S. B. Russell. The test was valuable in understanding the material fracture in ships during world war II.

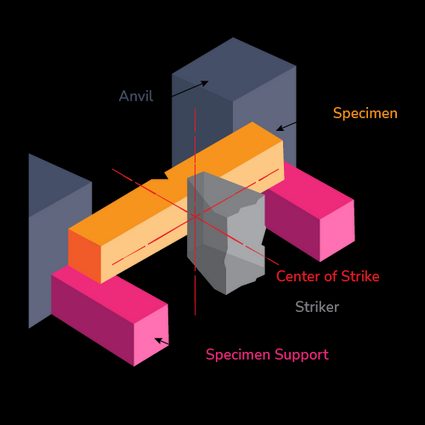
The Charpy test consists of a pendulum and a hammer of known mass attached to it. The pendulum swings and hits the notched specimen to observe the energy transfer. The results indicate the energy needed to fracture a material.

During the Charpy test, the specimen is fixed from either end, and the hammer strikes at the center. This contrasts with the Izod test, where the specimen is fixed as a cantilever beam. The test follows ASTM D6110 for plastics and E23 for metallic materials.

Let's use the impact test calculator to determine the fracture energy for a material specimen undergoing the Izod impact test. Use the following data:

Take:

• Angle of fall, $\alpha = 60°$;
• Angle of rise, $\beta = 30°$;
• Length of the pendulum distance to the center of the strike, $S = 1 \text{ m}$; and
• Mass of anvil, $m = 440 \text{ g}$.

To calculate energy absorbed:

1. Enter the angle of fall, $\alpha = 60°$.

2. Fill in the angle of rise, $\beta = 30°$.

3. Enter the mass of anvil, $m = 440 \text{ g}$.

4. Insert the length of pendulum distance to the center of the striker, $S = 1 \text{ m}$.

5. The calculator returns the initial and final heights, $h$ & $h_1$ as:

6. The impact test calculator returns the energy absorbed, $E$:

7. The impact velocity of the striker is:

You can use impact tests to calculate a material's fracture energy or impact resistance. In the test, a hammer strikes a fixed material specimen with a velocity to produce more than 2.7 J of energy. The energy causes the notched material specimens to break or bend.

The most common impact tests are Izod, and Charpy impact tests, which are pendulum-based. Other ways to assess material impact resistance are drop tower impact tests, ballistic impact tests, and high-speed plunder impact tests.

The alignment of material specimens varies between Izod and Charpy impact tests. Only the bottom half of the specimen is fixed in the Izod test, enacting a cantilever beam. In contrast, the specimens are fixed on either end in the Charpy test.

To calculate the impact velocity of the striker:

1. Subtract the cosine of the angle of fall from 1.
2. Multiply the difference with the length of pendulum distance to the center of strike.
3. Multiply the product with gravitational acceleration.
4. Multiply the answer by 2.
5. Find the square root of the product to obtain the impact velocity of the striker.

The impact velocity of the striker is 3.1316 m/s. Since the initial height is given, we can use it directly with the gravitational acceleration of 9.8067 m/s², the velocity of the striker becomes: √(2 × 9.8067 × 0.5) = 3.1316 m/s.