Last updated: Mar 24, 2024

Hydraulic Gradient Calculator

Q: What do you mean by hydraulic gradient?

The hydraulic gradient is the ratio of change in the hydraulic head and the distance between two points . It is a vector, and the direction of hydraulic gradient or head gradient gives you the direction of water movement while the magnitude tells us the significance.

Q: How do I calculate hydraulic gradient?

To calculate hydraulic gradient: Find the hydraulic heads , h₁, and h₂. Find the difference between hydraulic heads, Δh. Divide the difference by the distance between the two points to obtain the hydraulic gradient. Mathematically, this is: h_g = (h₁ - h₂)/L .

Q: What do you mean by positive hydraulic gradient?

A positive hydraulic gradient denotes an upwards flow whereas the negative hydraulic head gradient implies the flow is downwards . The sign tells us the movement of water in aquifers and underground. It is also helpful to draw potentiometer surface maps for areas of interest.

Q: What is the hydraulic gradient if the head varies 5 m over the length of 10 m?

The hydraulic gradient for the given condition is 0.5 m/m . The variation or difference in head is 5 m , i.e., Δh = 5 m , and the distance between two points is 10 m . Mathematically: h_g = Δh/L = 5 / 10 = 0.5 m .

New

Table of contents

Hydraulic gradient formula How to calculate hydraulic gradient FAQs

The hydraulic gradient calculator helps you determine the magnitude and direction of the water flow. It is a hydrogeological concept and is helpful in determining groundwater movement. You can also track the flow of contaminants using the same hydraulic gradient that causes the water to move or flow. You can also use the value of the hydraulic gradient in the hydraulic conductivity calculator to find out how much water flows through the soil.

The present article will briefly explain what a hydraulic gradient is and how to calculate a hydraulic gradient.

Hydraulic gradient formula

Before we get to the formula for hydraulic gradient, let's look at the hydraulic gradient.

The hydraulic gradient is the ratio of hydraulic head difference and the distance between two sample points (see distance calculator). In simple words, it tells us how the hydraulic head changes over a certain distance. If you plot the hydraulic head vs. distance on a graph, the hydraulic gradient is the slope of the line (cf. slope calculator). One can also define it as the change in water level per unit distance.

A hydraulic gradient is a vector quantity whose sign, or direction denotes the movement of water, i.e., if the sign is negative, it means the water flow is downwards. Whereas a positive hydraulic gradient signifies that the flow is upwards. For the heads, $h_1$ and $h_2$ at two points over a distance $l$ , the hydraulic gradient, $h_g$ is:

h_g = \frac{h_1 - h_2}{l}

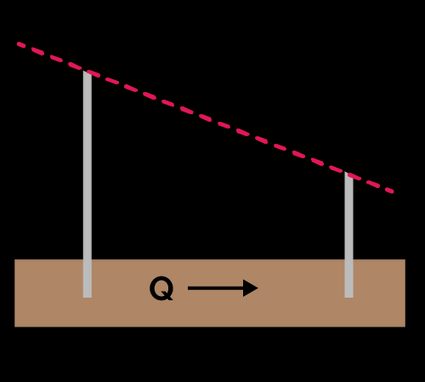
Change in head across a distance L is observable using hydraulic gradient.

How to calculate hydraulic gradient

Find the hydraulic gradient if the heads are 5 and 14 meters at points 1 and 2, respectively. The distance between the two points is 9 meters.

To calculate hydraulic gradient:

Enter the head at point 1, $h_1 = 5 \text{ m}$ .
Insert the head at point 2, $h_2 = 14 \text{ m}$ .
The calculator will return the change in head, $\Delta h = -9 \text{ m}$ .
Fill in the distance between points 1 and 2, $l = 9 \text{ m}$ .
The hydraulic gradient calculator will return the answer as:

\small \begin{align*} \qquad H_g &= \frac{h_1 - h_2}{l} \\\\ &= \frac{5 - 14}{9} = -1 \end{align*}

The answer $-1 \text{ m/m}$ implies the hydraulic head decreased $1 \text{ m}$ for every meter of distance from the point 1 and the water flow is downwards.

FAQs

What do you mean by hydraulic gradient?

The hydraulic gradient is the ratio of change in the hydraulic head and the distance between two points. It is a vector, and the direction of hydraulic gradient or head gradient gives you the direction of water movement while the magnitude tells us the significance.

How do I calculate hydraulic gradient?

To calculate hydraulic gradient:

Find the hydraulic heads, h₁, and h₂.
Find the difference between hydraulic heads, Δh.
Divide the difference by the distance between the two points to obtain the hydraulic gradient. Mathematically, this is: h_g = (h₁ - h₂)/L.

What do you mean by positive hydraulic gradient?

A positive hydraulic gradient denotes an upwards flow whereas the negative hydraulic head gradient implies the flow is downwards. The sign tells us the movement of water in aquifers and underground. It is also helpful to draw potentiometer surface maps for areas of interest.

What is the hydraulic gradient if the head varies 5 m over the length of 10 m?

The hydraulic gradient for the given condition is 0.5 m/m. The variation or difference in head is 5 m, i.e., Δh = 5 m, and the distance between two points is 10 m. Mathematically:

h_g = Δh/L = 5 / 10 = 0.5 m.