Density Altitude Calculator

Omni's density altitude calculator will tell you the effective altitude of your plane compared to the ICAO International Standard Atmosphere standard conditions. This is important to know for airplane engine and aerodynamic performance.

In this article, we will explain the density altitude definition, the density altitude formula, and how to use our air density altitude calculator.

The density altitude is another way of expressing air density, and is mainly used in the aviation industry by pilots. Engine performance and aerodynamic lift are very dependent on air density. Too little, and the engine may struggle to provide enough forward thrust and the wings enough lift, which could spell trouble for a smooth plane journey.

Density altitude is the calculated altitude based on the ICAO International Stand Atmosphere (ISA) model (ICAO stands for the International Civil Aviation Organization). At zero altitude, this model sets the air temperature to 15 °C (59 °F), air pressure to 1013.25 mbar (29.921 inHg, and if you don't remember the conversion between these units, visit our pressure converter), relative humidity to 0%, and air density to 1.225 kg/m³ (0.076474 lb/ft³).

In the model, as you go up in altitude, the air gets less dense, and the air pressure decreases — as you can see in the air pressure at altitude calculator. Therefore, you can relate altitude to air density. Of course, the real world will hardly ever have the same atmospheric conditions as the standard model. This means there will most probably be a difference between your density altitude and the air's real density around the plane.

Finding the density altitude means calculating the equivalent height in the ISA model that has the same air density as the air currently around the plane. We can then use the density altitude (A.K.A. air density) to predict plane engine performance and how much lift the wings will generate. It is also one of the parameters we use in the true airspeed calculator, a handy tool for aviation.

Traditionally, a pilot would keep a density altitude chart in the cockpit of their plane to look up the density altitude. Here is an example of one:

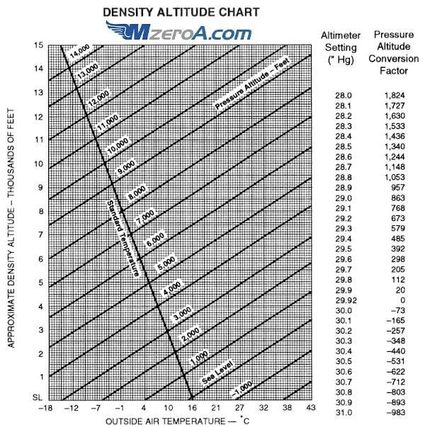
You use this chart in the following manner:

1. Lookup a weather report from the nearest weather station to get the latest altimeter setting.
2. Read off the corresponding pressure altitude conversion factor from the list of numbers to the right of the graph. Add the elevation of the weather station to this conversion factor.
3. Find the current air temperature on the x-axis of the graph and travel upwards until you get to the value of pressure altitude (conversion factor plus station elevation), using the lines labelled with pressure altitude.
4. Read across to the y-axis to find the density altitude.

Of course, it might be a lot simpler to use our air density altitude calculator instead (though having a paper chart as a backup is also a good idea when in flight). We also plot a graph of the pressure altitude line you are currently on, just like you see in the chart.

Let's now look at how to find density altitude. The density altitude calculation formula finds the density altitude (or geopotential altitude) $H$ in $\mathrm{km}$ in terms of only one variable, the air density $ρ$ in $\mathrm{kg/m^3}$:

The constants in the equation above are derived from the ISA model's constants stated in the previous section.

We can now use Omni's air density calculator to calculate the air density at a given dry air pressure, water vapor pressure (i.e., humidity), and temperature, using the equation:

Where:

• $P_{\mathrm{d}}$ — The pressure of dry air in Pascals;
• $P_{\mathrm{v}}$ — The water vapor pressure in Pascals;
• $T$ — The air temperature in Kelvins;
• $P_{\mathrm{d}}$ — The specific gas constant for dry air equal to $287.058\ \mathrm{J/(kg\cdot K)}$; and
• $P_{\mathrm{v}}$ — The specific gas constant for water vapor equal to $461.495\ \mathrm{J/(kg\cdot K)}$.

The water vapor pressure $P_{\mathrm{v}}$ can be calculated from the air temperature and relative humidity using the equation:

The actual air pressure is the sum of the dry air pressure and the water vapor pressure:

We can use weather reports to calculate a value for the air pressure. An altimeter setting and weather station elevation in an aviation weather report is what we need to determine the air pressure accurately. The altimeter setting is the value in the Kollsman window of an altimeter. It is used to correct a plane's altimeter for air pressure changes due to weather.

The air pressure can be found from the altimeter setting and weather station height using the equation:

Where:

• $P$ is the air pressure, in millibars ($\mathrm{mbar}$);
• $A_{\mathrm{S}}$ is the altimeter setting ($\mathrm{mbar}$); and
• $h$ is the weather station elevation ($\mathrm{m}$).

Let us now explain the simple steps you need to follow to calculate your density altitude using Omni's density altitude calculator.

1. Input the outside air temperature.
2. The next step is to specify the moisture content of the air. You can either enter the dewpoint temperature or the relative humidity depending on which one you know. Note, that the dew point can not be higher than the temperature, and relative humidity cannot be greater than 100%.
3. Input your altimeter setting. You can get this value from a recent weather report. Use the value from the nearest weather station.
4. From the same weather report, enter the elevation of the weather station.
5. You will then see a result for your density altitude.
6. We also calculate the air density, relative density, and absolute air pressure, so you have all the data you need.
7. You'll also see a graph of temperature vs. density altitude for your current pressure altitude.

You'll now have a better understanding of your plane's engine performance and the amount of lift you get from its wings, thanks to converting the current conditions to an altitude based on the standard atmosphere model.

Let's go through an example of calculating the density altitude. A recent weather report from a weather station with an elevation of $1,500\ \mathrm{m}$ ($4,921\ \mathrm{ft}$) gives an altimeter setting of $990\ \mathrm{mbar}$ ($29.24\ \mathrm{in\ Hg}$). The air temperature is $33\ \mathrm{\degree C}$ ($91\ \mathrm{\degree F}$) and the dew point is $18\ \mathrm{\degree C}$ ($65\ \mathrm{\degree F}$) - using Omni's dew point calculator, the relative humidity is therefore $41\\%$.

First, we calculate the air pressure:

Then calculate the water vapor pressure $P_{\mathrm{v}}$:

Therefore, the value of $P_{\mathrm{d}}$ is $P - P_{\mathrm{v}} = 825.48\ \mathrm{mbar} - 20.62\ \mathrm{mbar} = 804.86\ \mathrm{mbar}$. We can now calculate the air density using the equation defined above and by converting pressure and temperature units:

The final step is to input this air density into the density altitude equation: